Индекс соответствует оси, которой они параллельны

Касательные напряжения при поперечном изгибе. Формула Журавского.

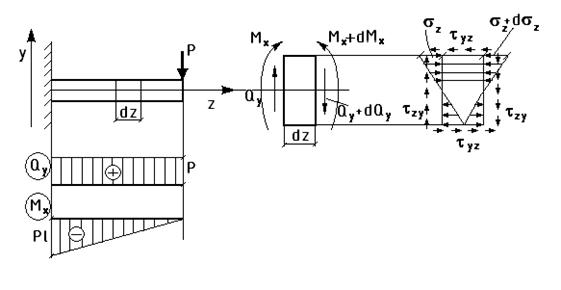
Касательные напряжения ввиду своей парности всегда именуются двумя индексами: 1-й индекс соответствует той оси, которой они перпендикулярны,

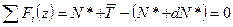
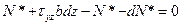
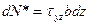
	(1)
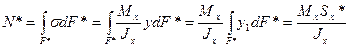
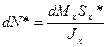
	(2)

(1)=(2):

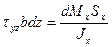
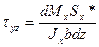
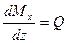
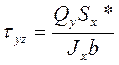- формула Журавского

Q_y – поперечная сила – const для любой точки поперечного сечения;

J_x – момент инерции сечения – постоянная величина для всего сечения относительно оси Х;

b – ширина сечения в рассматриваемой точке, b≠const;

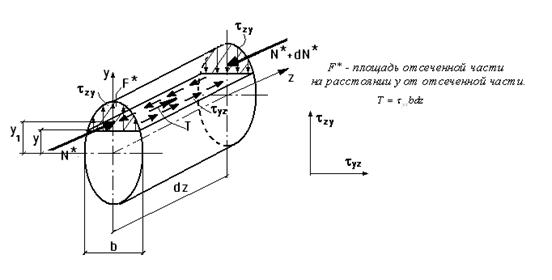
S_x* - статический момент отсеченной части сечения площадью F*:

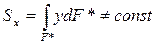
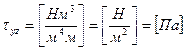
Максимального значения касательные напряжения достигают в центре тяжести сечения: статический момент максимален из-за максимального значения площади F*.

Минимального значения касательные напряжения достигают по верхней и нижней границе сечения.

Пример:

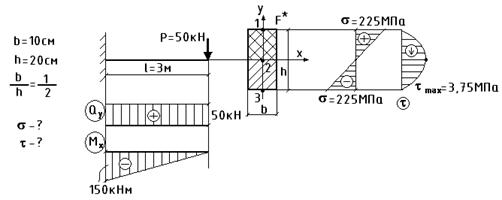
Опасное сечение – заделка.

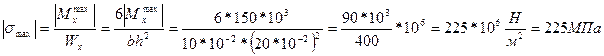
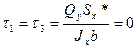
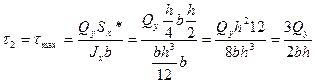
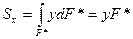(для прямоугольника)

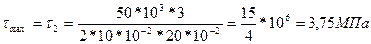
При проведении прочностных расчетов из-за малости касательных напряжений ими часто пренебрегают.

Формула Журавского справедлива для достаточно узких и высоких профилей балки: b<<h, т.к. предполагается, что касательные напряжения равномерно распределены по ширине сечения, что подтверждается экспериментально.

Для балок иных профилей формула Журавского носит приближенный характер