Закон парности касательных напряжений

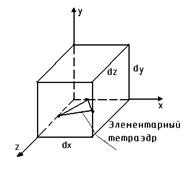
Напряженное состояние в окрестности точек тела и его виды.

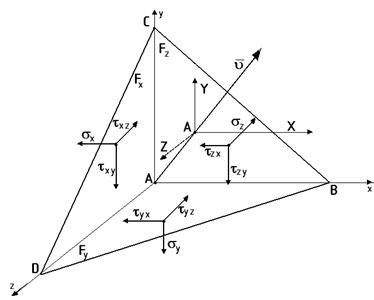
Совокупность напряжений, действующих на различные площадки, проведенных через точки тела, характеризует напряженное состояние в окрестности данной точки.

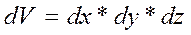
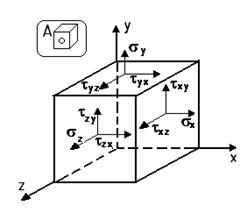
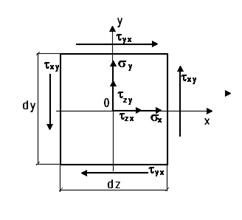
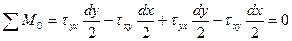
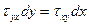
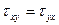
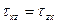
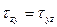
Касательные напряжения по двум взаимно перпендикулярным площадкам всегда равны по величине и направлены навстречу друг другу или наоборот.

Напряженное состояние в точке определяется 6 компонентами: σ_x, σ_y, σ_z, τ_xy=τ_yx, τ_yz=τ_zy, τ_zx=τ_xz.

Тензор напряжения – матрица вида:

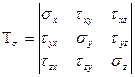
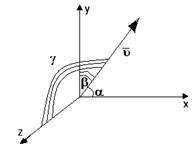
ν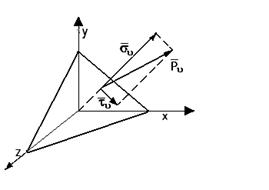 - внешняя нормаль к наклонной площадке;

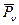- вектор полного напряжения;

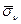- вектор нормального напряжения;

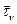- вектор касательного напряжения.

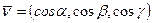
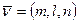
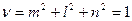
Теорией упругости доказывается:

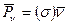или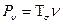

X, Y, Z – проекции вектора на оси x, y, z.

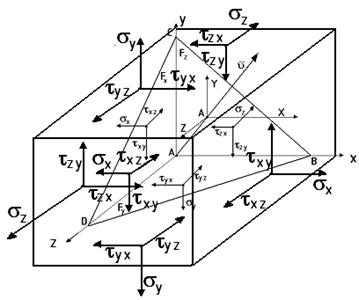
Обозначим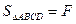

Площадь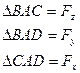

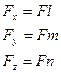
Спроектируем все силы на соответственные оси координат:

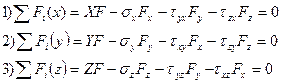
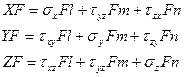
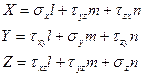- формула для

вычисления проекции вектора напряжения на оси x, y z.

Предположим, что наклонная площадка BCD является главной (отсутствуют наклонные напряжения).

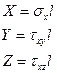- σ_x, σ_y, σ_z переобозначим как S; следовательно σ_x=S, σ_y=S, σ_z=S – являются главными напряжениями.

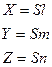
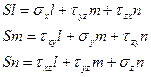
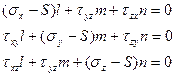
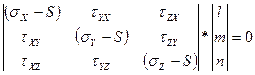
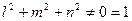
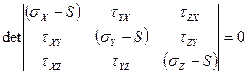
S – 3 корня кубического уравнения, которые представляют собой главные напряжения.

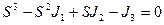
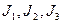- инварианты

σ₁≥ σ₂≥ σ₃ - индексы главным напряжениям присваиваются в порядке убывания их величин с учетом знака.

Инварианты – это величины, не изменяющиеся при любом наклоне площадки.

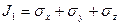
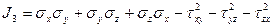
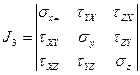
Если все 3 инварианта отличны от нуля, то напряжение называется объемным.

Если 2 инварианта отличны от нуля, а третье равно нулю, то напряжение называется плоским.

Если 1 инвариант отличен от нуля, а два равно нулю, то напряжение называется линейным напряженным состоянием.

Инварианты могут быть как положительными, так и отрицательными величинами.

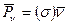или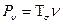

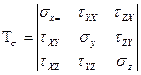
Существует 3 вида напряженного состояния:

1. односложное (линейное): одно из главных напряжений не равно нулю, а два других равны нулю;

2. двухосное (плоское): два главных напряжения не равны нулю, одно равно нулю.

3. трехосное (объемное): все три главных напряжения отличны от нуля.