Равноточной величины

Постановка задачи. Описательная статистика. Классическая задача оценивания.Задача эталонирования.

Постановка задачи. Наличие избыточных (п –1) измерений при многократных измерениях одной величины, приводит к неоднозначным результатам с одной стороны, а с другой позволяет провести контроль и выполнить оценку точности на основе статистических методов. Таким образом, задача оценивания результатов многократно измеренной величины сводится к оценке количественной стороны (оценка математического ожидания) и качественной (оценка меры разброса). При этом, обычно используют как точечные, так и интервальные оценки. Следует иметь ввиду, что, по сути задачи – наличие неопределенности в результатах измерений, – предпочтительнее интервальная оценка. Но ее качество очень зависит от точности знания закона распределения погрешностей измерений и числа измерений.

Выделим следующие походы к решению задачи оценивания результатов многократного измерения одной величины:

1. Классический случай.

Здесь предполагается, что закон распределения погрешностей измерений достаточно нормальный, чтобы использовать основные характеристики, соответствующие этому закону. Кроме того, предполагается отсутствие значимых мешающих параметров – грубых и систематических погрешностей.

2. Анализируемый классический случай.

В этом случае, по мере возможности, проводится исследование на соответствие нормальному закону распределения погрешностей измерений. Проводится анализ на наличие грубых и значимых систематических влияний. Только после этого выносится суждение об использовании формул оценивания.

3. Неклассические методы оценивания.

Если результаты исследований (см. п. 2) дали наличие группы «сомнительных» измерений (еще не грубые, но уже и не нормальные, причем не одно), наличие в каком либо виде значимого систематического влияния или заметное отличие от нормального закона, то используют разного рода неклассические алгоритмы обработки. К ним, для перечисленных случаев можно отнести:

– обобщенный метод наименьших квадратов (ОМНК), учитывающий неравноточность (гетероскедастичность) и коррелированность (автокорреляцию) результатов измерений в виде ковариационной матрицы, но в рамках нормального закона распределения. Частный случай его, при наличии только неравноточности, взвешенный метод наименьших квадратов (ВМНК) с диагональной ковариационной матрицей предложен ещё Гауссом.

– робастные (помехоустойчивые) процедуры, позволяющие при наличии «сомнительных» измерений и незнании точного закона распределения, а только его класса, получать достаточно устойчивые и асимптотически эффективные оценки.

– параметрические неклассические оценки, в которых производится исследование на соответствие какому-либо закону распределения, а затем по методу максимального правдоподобия или методу моментов или какому либо другому методу, получают вид оценок, оптимальный для выявленного вида распределения.

– непараметрические методы оценивания, позволяющие получать оценки, совсем не зная закона распределения. При этом ставиться условие, чтобы они были не сильно хуже параметрических, когда закон распределения известен, и асимптотически эффективные в противном случае.

– адаптивные оценки – оценки на основе индикаторов. В качестве индикатора может быть какая-либо характеристика результата измерений, по значению которого делается вывод об использовании того или иного вида оценок – разветвление. Часто в этом классе используется простой перебор оценок с изменением каких либо параметров процедуры оценивания и по какому либо критерию выбирают оптимальную.

Описательная статистика. Традиционно, но не обязательно, перед началом детальной обработки результатов измерений представляется описательная статистика. В неё включают обычно следующие пункты: число наблюдений, минимальное и максимальное значение, среднее и медиана, смещенная и несмещенная оценка дисперсии, смещенная и несмещенная средняя квадратическая погрешности, асимметрия и эксцесс, коэффициент вариации, сумма всех элементов, сумма квадратов отклонений от среднего, сумма квадратов значений, автокорреляция 1-го порядка. Где возможно получают уровень значимости величины.

Описательная статистика призвана давать первое представление о ряде измерений и поведении его основных характеристик, а также служить основой для дальнейших, более детальных вычислений и исследований.

Классическая задача оценивания. Для этого случая априорно предполагается закон распределения результатов измерений достаточно нормальным и отсутствие значимых грубых и систематических влияний:

.

В теории оценивания для этого случая (см. гл. 1. 4) было показано, что оценка математического ожидания есть обычное среднее арифметическое 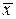, а оценка стандарта, как меры рассеивания, есть средняя квадратическая погрешность т по Бесселю или по Гауссу. Рассматривая подход Хьюбера для получения М – оценок (см. (1.6.15) и т.д.) было показано, что целевая функция для результатов измерений с нормальным законом распределения погрешностей имеет вид 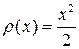. Метод максимального правдоподобия для получения эффективных оценок, требует минимизации этой функции. Таким образом, если имеется п результатов измерений величины о которой известно, что погрешности ее измерений распределены нормально, то для получения «наилучшей» оценки наиболее надежного значения, необходимо минимизировать следующую целевую функцию (функцию потерь)

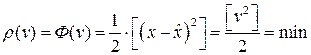. (4.1.1)

Здесь 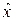– неизвестная оценка сдвига (математического ожидания). Коэффициент ½ не играет никакой роли и поэтому может быть даже удален. Поиск минимума дает уравнение

.

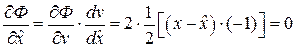Удаляя постоянную в однородном уравнении (которое не влияет на результат) и раскрывая сумму, имеем

,

или

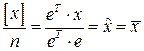. (4.1.2)

Здесь е – вектор-сумматор в виде столбца из п единиц. То есть, мы опять получили для оценки математического ожидания при нормальном законе распределения погрешностей результатов измерений, обычное среднее арифметическое.

Таким образом, на первом этапе обработки одной многократно измеренной равноточной величины, получаем в качестве основных точечных характеристик среднее арифметическое 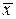и среднюю квадратическую погрешность т. Следующий этап – оценка качества полученных величин. Для этого в первую очередь получаем среднюю квадратическую погрешность среднего арифметического 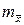. Мы получали его и используя свойства дисперсии и как среднюю квадратическую погрешность функции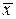

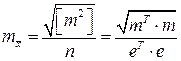(4.1.3)

или

, (4.1.3а)

где т – вектор-столбец их погрешностей измерений; т ₀ – средняя квадратическая погрешность одного измерения, в случае если они все примерно одинаковы. Таким образом, погрешность одного измерения в 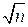раз больше чем погрешность среднего арифметического. Погрешность определения средней квадратической погрешности 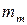также описана ранее, как

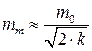, (4.1.4)

где k – число степеней свободны, равное п если средняя квадратическая погрешность одного измерения определялась по формуле Гаусса и k = n – 1 если погрешность m определялась по формуле Бесселя.

Следует учесть, что в качестве меры рассеивания получают дисперсию с неудобной квадратической размерностью. Но переход от неё к стандарту 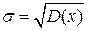– путем извлечения корня, операция нелинейная и приводит к смещению оценки меры рассеивания в виде стандарта. Это смещение должно быть учтено, хотя оценка и остается состоятельной и асимптотически эффективной. Тогда несмещенные оценки есть:

для формулы Гаусса (т.е. при известном математическом ожидании)

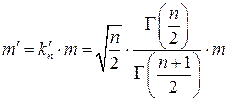; (4.1.5)

для формулы Бесселя, (математические ожидание неизвестно, но есть его оценка в виде среднего арифметического)

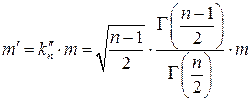. (4.1.5а)

Здесь Г(х) – гамма- функция Эйлер а со свойствами

Г(п + 1) = п Г(п); Г(п) = (п – 1)!; Г(1) = Г(2) = 1;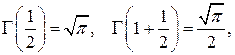

.

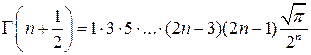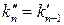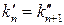Можно доказать, что , или . При 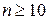можно использовать приближенное разложение для коэффициента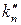

. (4.1.6)

При 4 £ n £ 9 это выражение также можно использовать, если требуется невысокая точность (не более 1%). При высокой точности используют формулы или Таблицу4.1.1