Основні поняття про електричне поле

Л_18

Откуда

Таблица корректировочных множителей

Таблица 4.1.1

n
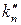
	1.085	1.064	1.051	1.042	1.036	1.032

При получении основных характеристик выделяют следующие случаи: известно математическое ожидание – задача эталонирования, неизвестно математическое ожидание – задача оценивания; известна дисперсия, неизвестна дисперсия.

Если известна дисперсия, то,

известно математическое ожидание, то искомая оценка дисперсии есть 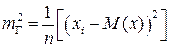, неизвестно математическое ожидание, тогда оценка дисперсии есть 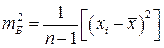. Дисперсии этих оценок будут соответственно .

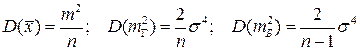Интервальные оценки основных характеристик (см., например, [18]). При построении доверительного интервала для оценки математического ожидания при нормальном законе распределения погрешностей измерений выделяют два случая: стандарт s известен и стандарт s оценен s» m. В первом случае известно, что доброкачественная (несмещенная, состоятельная и эффективная) оценка математического ожидания есть среднее арифметическое 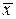с параметрами 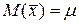, 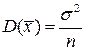. Нормированное отношение 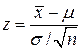распределено также нормально с параметрами m = 0, s ²= 1. Поэтому вероятность любого отклонения 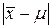можно вычислить по формуле

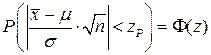. (4.1.7)

Задавая доверительную вероятность 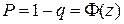по таблицам распределения Гаусса (Приложение 1, или 5) определяем значение квантиля z_P. Для оценки m преобразуем формулу (4.1.7)

,

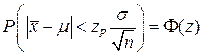или

,

откуда получим

. (4.1.8)

Таким образом, с вероятностью (надежностью) 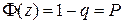можно утверждать, что интервал 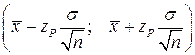является доверительным для оценки m.

Обозначим 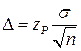. При фиксированном значении z_P с возрастанием n D уменьшается и точность интервальной оценки увеличивается. Увеличение же надежности оценки 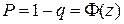ведет к увеличению z_P (Ф(z) – функция возрастающая), поэтому при фиксированном объеме n величина D также возрастает, что ведет к увеличению доверительного интервала и уменьшению точности оценки.

Если выбрана доверительная вероятность Р, то это значит, что если произведено достаточно большое количество выборок из генеральной совокупности, то P % из них определяют такие доверительные границы, внутри которых будет находиться оцениваемый параметр m, и лишь 1 – P % интервалов его не содержит. Поэтому, было бы ошибкой толковать равенство 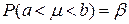как вероятность того, что математическое ожидание заключено в интервале [ a, b ]. Математическое ожидание может лишь попасть в этот интервал, и тогда вероятность этого события равна единице, либо не попасть, тогда вероятность события ноль. Следовательно, доверительную вероятность не следует связывать с оцениваемым параметром – она связана лишь с границами интервала, определяемыми случайностью выборки.

Если при доверительном оценивании стандарт не известен, а есть его оценка в виде средней квадратической погрешности m, то для построения интервала для неизвестного математического ожидания m используют случайную величину

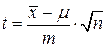
Эта величина, как было показано выше, распределена по закону Стьюдента. Поэтому, выбрав вероятность P =1– q и, зная объем выборки n, по таблицам Стьюдента (см. Приложение 6), находят t_n,P, такое что

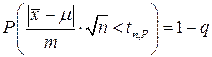. (4.1.9)

Преобразуя формулу для оценки m, имеем

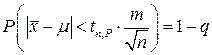
или

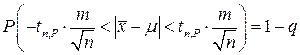
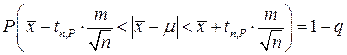, (4.1.10)

а интервал

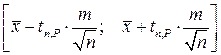(4.1.10а)

с надежностью (вероятностью) P является доверительным для оценки m. Заметим, что в этом случае для построения доверительного интервала коэффициент t_n,P зависит как от доверительной вероятности, так и от объема выборки n. Обычно при малом n интервал на основе закона Стьюдента для оценки математического ожидания более широкий, чем при использовании нормального закона распределения. Это не говорит о недостатке распределения Стьюдента, а скорее о его преимуществе, так как при использовании t- распределения учитывается, что никакой дополнительной информации о неизвестной дисперсии s ² кроме той, которую дает выборка нет. Использование же при малом n и неизвестной дисперсии для интервальной оценки математического ожидания нормального закона распределения привело бы к неоправданному сужению доверительного интервала.

Рассмотрим построение доверительного интервала для дисперсии s ² по выборочной дисперсии m², полученной по n измерениям с нормальным распределением погрешностей. Выбираем доверительную вероятность P =1– q. Ранее было показано, что величина (n×m ²) / s ² имеет распределение c ² с k = n – 1 степенями свободы. Тогда можно записать

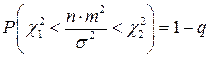. (4.1.11)

По таблицам c ² – распределение (см. Приложение 7) нужно выбрать такие два значения 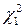и 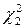, чтобы площадь, заключенная под дифференциальной функцией распределения c ² между 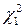и 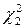была равна 1 – q

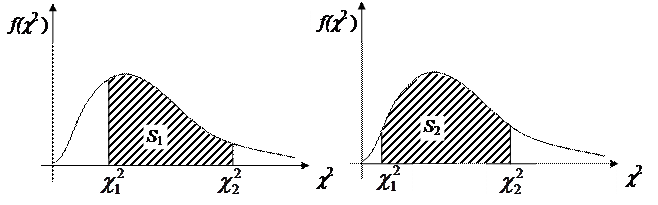
Рис. 4.1. Доверительная область для c ² – распределения.

Из рис. 4.1 очевидно, что значениям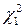и и 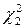можно варьировать так, чтобы значение заштрихованной площади (вероятности), оставалось постоянной (S ₁ = S ₂) и равной P =1– q. Но обычно 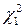и 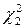выбирают так, чтобы

,

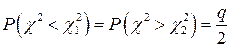то есть площади не заштрихованные (краевые) на рис. 4.1 были равны между собой. Тогда имеем

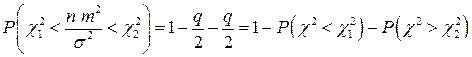. (4.1.12)

Для вычисления левой границы используем тождество

,

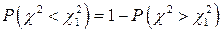так как таких вероятностей в таблице распределения 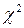нет. Поэтому

.

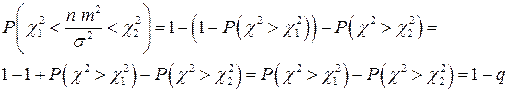Итак,

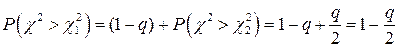. (4.1.13)

Преобразуем двойное неравенство 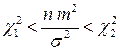так, чтобы можно было оценить 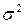. Рассмотрим два эквивалентных ему неравенства 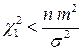и 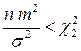, откуда находим границы 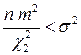и 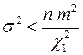. Обобщая результаты можно записать

, (4.1.14)

или

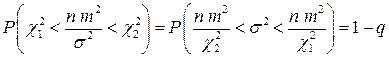. (4.1.14а)

Таким образом, доверительный интервал для дисперсии 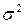имеет вид

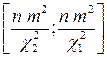. (4.1.14б)

Здесь определены интервалы для оценки дисперсии по формуле Гаусса. Если используется формула Бесселя, (что в практике встречается чаще) применяют (п – 1) степень свободы.

При оценивании стандарта 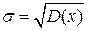, интервал примет вид:

для оценки средней квадратической погрешности по формуле Бесселя

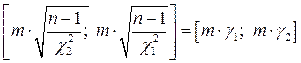; (4.1.15)

для оценки средней квадратической погрешности по формуле Гаусса

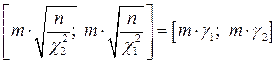. (4.1.15а)

Практически поступают следующим образом. Задают доверительную вероятность P = 1 – q. Так как 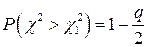, а 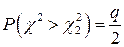, находят 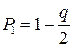и 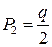. По этим значениям вероятности и по таблицам c ² – распределения с п – 1 (или п)(см. Приложение 7) степенями свободы, находят 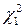и 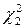, по которым и строят доверительные интервалы.

Если необходимо произвести доверительное оценивание средней квадратической погрешности среднего арифметического 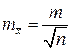, то границы интервалов, полученных ранее, делят на 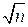и доверительный интервал для оценки 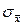будет

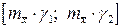. (4.1.15б)

Таким образом, последовательность обработки одной многократно измеренной равноточной величины можно свести к следующей:

1. Вычисление точечной оценки математического ожидания как среднего арифметического и погрешности одного измерения по формуле Бесселя

.

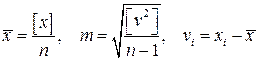Контролем служит равенство нулю суммы квадратов уклонений от среднего .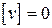

2. Оценка качества точечных оценок в виде погрешности среднего арифметического и погрешности одного измерения

.

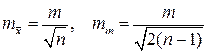3. Построение интервальных оценок (формулы (4.1.10), (4.1.14), (4.1.15)) для 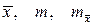, с доверительной вероятностью P (как оценок теоретических значений ):

,

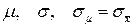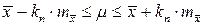где k_n = z_P при известном стандарте и k_n = t_n,P при неизвестном,

,

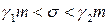где g₁ и g₂ зависят от вида формулы оценивания стандарта;

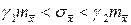
Понятие веса измерения. Разного рода погрешности являются абсолютными мерами точности результатов измерений и их функций. Однако часто в практике оказывается нужным знать во сколько раз один из результатов измерений точнее какого либо другого. В качестве такой меры относительной точности в теории погрешностей измерений принята величина, называемая весом (Р. Коутс, 1700 г). Таким образом, веса – специальные характеристики относительной точности результатов измерений и их функций, получаемые как величины, обратно пропорциональные абсолютным мерам точности. Для нормального закона распределения эти величины обратно пропорциональны квадрату средней квадратической погрешности (оценке дисперсии). Исходя из этого, веса показывают степень неравноточности результатов измерений или степень не одинаковости условий измерений и являются степенью доверия к i- товому измерению. Так, если имеется ряд результатов измерений х ₁, х ₂, …, х_п с соответствующими погрешностями результатов измерений в виде т ₁, т ₂, …, т_п,то веса, характеризующие их относительную точность есть

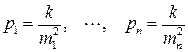, (4.5.1)

где k – общий коэффициент пропорциональности, который может быть произвольным. Очевидно, что произвольность k приводит к условности понятия веса измерения, но только для его абсолютной формы (4.5.1). В относительной форме (например, при соотношении весов измерений и т. д.), этот коэффициент не влияет на результаты и понятие веса оказывается весьма полезным и удобным. Не сложно заметить, что выбор коэффициента k равным квадрату средней квадратической погрешности некоторого i- тового результата измерения, равносилен принятию веса этого результата за единицу. Тогда все остальные веса будут пропорциональны погрешностям i- тового измерения.

Например, 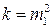. Тогда

.

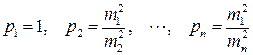Если известны коэффициенты пропорциональности между погрешностями первого и i-тового измерения 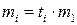, то веса в этом случае будут

.

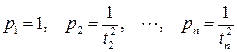Это возможно произвести по отношению не только первого, но и любого i-тового измерения.

Из (4.5.1), приняв вес равный единице получим, что 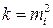. Обозначив через m среднюю квадратическую погрешность результата измерения вес которого равен единице вид веса представляют как

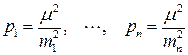. (4.5.1а)

Величину m условно называют стандартом единицы веса, а ее оценку – средней квадратической погрешностью единицы веса, так как она соответствует погрешности, вес которого равен единице.

Одним из главных достоинств весов, как показателей точности результатов измерений есть то, что очень часто их можно вычислить, даже если неизвестны стандарты результатов измерений или их оценки в виде средней квадратической погрешности. Это приводит к некоторому искажению, приближенности весов.

Например, если измерен угол в п приемов, то его средняя квадратическая погрешность есть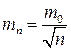, а вес по (4.5.1)

.

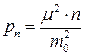Полагая за погрешность единицы веса погрешность одного измерения , имеем 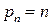. Очень часто, без видимого ущерба для точности, принимают, что 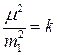. Тогда вес будет 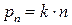, где k – произвольно.

Средняя квадратическая погрешность нивелирного хода длиною в L километров есть 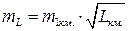, а его вес из (4.5.1) есть 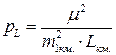. Приняв 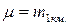, имеем значение веса 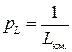. Если опять определить, что , то имеем 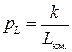, где k – произвольно и т. д.

При вычислении веса достаточно удерживать две значащие цифры.

Если результаты измерений умножить на корень квадратный из его веса, то полученный результат будет иметь вес, равный единице. На этом основано приведение не равноточных измерений к равноточным.

Например, угол b измерен п раз с погрешностями т_i. Вес i-тового измерения есть 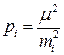(см. (4.5.1а)). Если результаты измерений домножить на 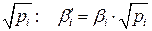, то их веса будут равны 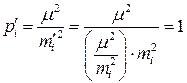, что и требовалось доказать.

Рассматривая вопрос надежности получения весов, используют формулу

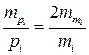(4.5.2)

откуда, из значения для 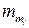имеем

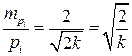, (4.5.2а)

где k = n для определения средней квадратической погрешности по формуле Гаусса и k = (n – 1) для формулы Бесселя. Отсюда следует, что приближенные веса в два раза менее надежные чем соответствующие средние квадратические погрешности.

Если известен вес измерения, то из (4.5.1) его погрешность будет

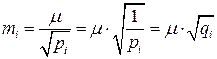. (4.5.3)

Здесь величины q_i называют обратными весами измерений.

Среднее весовое из результатов неравноточных измерений. Различие точностей измерений естественно предполагает учет этих измерений, при их использовании для определения наиболее надежного значения из ряда не равноточных измерений, с разными весами, так как результаты измерений получены в разных условиях (например, имеют разные средние квадратические погрешности т_i). Получим вид формулы наиболее надежного значения исходя из принципа Лагранжа. Пусть наиболее надежное значение будет представлено в виде линейной комбинации результатов измерений x_i с коэффициентами k_i

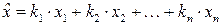. (4.5.4)

Наложим условие на коэффициенты k_i: сумма коэффициентов равна 1: [ k ] = 1. Это следует из того, что при одинаковых значениях x_i должно быть 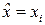, что будет только при наложенном выше условии. С другой стороны, если все коэффициенты k_i равны между собой, то k_i = 1/ п и 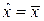, что и должно быть на самом деле. Найдем оценку дисперсии функции (4.5.4)

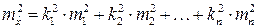. (4.5.4а)

Теперь поставим задачу, что хотим найти минимум (4.5.4а) при наложенном условии, что совершенно очевидно, и найдем вид коэффициентов k_i приводящих к наилучшим оценкам (наименьшей дисперсии) наиболее надежного результата. Для этого используем метод неопределенных множителей Лагранжа поиска условного экстремума для целевой функции вида

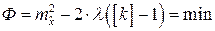. (4.5.5)

Здесь l – неопределенный множитель Лагранжа, принадлежащий условию [ k ] = 1, которое должно быть обнулено. Так как ищется вид коэффициентов k_i, то производные от целевой функции (4.5.5) берутся по ним и полученные выражения приравниваются к нулю

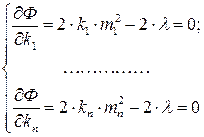, (4.5.6)

Откуда

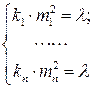, (4.5.6а)

а

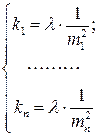. (4.5.6б)

Теперь необходимо найти коэффициент l. Для этого воспользуемся условием [ k ] = 1 и сложим левую и правую части (4.5.6б)

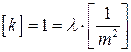, (4.5.7)

откуда

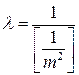, (4.5.7а)

а

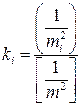. (4.5.7б)

Обозначив 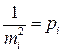(см. (4.5.1)) формула (4.5.4) примет вид

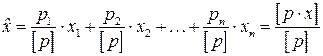, (4.5.8)

или в матричном виде [10]

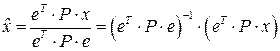. (4.5.8а)

Здесь е – вектор-столбец (сумматор) из единиц.

Ще давні греки знали, що янтар потертий об хутро отримує здатність притягувати до себе пух, волосся та інші легкі тіла, але зовсім не знали у чому суттєвість цього явища та чим воно може бути корисним для людства. Грецький філософ Фалес Мілетський у VI столітті до нашої ери описав це явище, яке більш ніж 2000 років залишалось не вивченим. У XVI столітті англійський вчений Гілберт повторив досліди, описані Фалесом Мілетським. На базі дослідів він встановив, що крім янтарю, властивість притягувати легкі тіла отримують при терті алмаз, гірський кришталь, сірка, смола… Тіла, які володіють подібними властивостями почали називати наелектризованими.

Слово «електрика» походе від слова «електрон», що грецькою мовою означає янтар. А явище виникнення цих властивостей у тіл було названо електризацією. Доказ електризації металів тертям уперше було дано руським фізіком В.В.Петровим. Виявилось, що наелектризувати тертям можна всяке тіло не залежно від того в якому воно стані: твердому, рідкому чи газоподібному.

Дюфе у 1733 році виявив, що тіла електризуються різнорідними електриками: перший рід з’являється на склі, дорогоцінних каменях, хутрі, другий - на янтарі, смолі, шовку. Пізніше електрику, яка з’являється на склі, назвали позитивною, а на янтарю - негативною.

Таким чином, всяке тіло вміщує у себе багату кількість елементарних часток речовини, які мають електричний заряд: позитивний (протони) чи негативний

(електрони). Коли тіло має однакову кількість протонів й електронів, то кажуть, що воно електрично нейтральне. В електрично зарядженому тілі переважають ті чи інші заряди, й тоді кажуть, що тіло позитивно чи негативно заряджене.

Заряди (чи електрично заряджені тіла) взаємодіють між собою на відстані: різнойменні заряджені частки притягуються один до одного ("+ та -"), однойменні заряджені частки відштовхуються один від одного ("- та -" чи "+ та +"). Цю властивість зарядів назвали законом взаємодії зарядів.

Таким чином, заряд - це властивість та міра наелектризованості тіла. Електричний заряд позначають - q, Кл (кулон). Електричний заряд електрона: q = 1,6 × 10^-19 Кл. Тобто, при числі електронів 6,3 × 10¹⁸ q = 1 Кл та його називають одиничним зарядом. Заряд розміщується тільки на поверхні.

Електричне поле - це матеріальне середовище, яке оточує заряди, в якому заряди взаємодіють між собою і яке неможливо відчути органами почуття.

Кожний заряд пов’язаний з оточуючим його електричним полем. Електричне поле чинить силову дію на внесене в нього електричне заряджене тіло. Тобто електричне поле виконує роботу по відношенню до внесеного тіла, та володіє енергією, яку називають електричною.

Електрична енергія - це властивість електричного поля виконувати роботу по відношенню до внесеного в нього електрично зарядженого тіла чи часток. Позначається - W, Дж.