Поиск решений в игровых программах

Рассмотрим класс игр, которые характеризуются как игры с полной информацией о текущей игровой ситуации, где два игрока-противника по очереди делают ходы. Успех одного игрока – такая же по величине потеря для другого игрока (игры с нулевыми суммами). Допустимые ходы игры определяются конечным набором правил, которые исключают случайность. Игра начинается из специфического начального положения и завершается победой того или иного игрока либо ничьей.

При рассмотрении игровых программ игроком считается компьютер, а противником – человек. Сложность поиска решений в игровых деревьях весьма высока, так как вершины имеют высокую степень разветвления. Например, в середине шахматной партии игрок может сделать около 35 ходов, разрешенных правилами. Общее количество вершин дерева игры в шахматы оценивается значением 10 в 120-й степени.

Если предположить, что можно обследовать 10 в 9 степени вершин в секунду, то построение полного дерева игры в шахматы заняло бы 10 в 103 степени лет, поэтому полный просмотр такого дерева невозможен. В силу этого в игровых деревьях используют следующие приемы:

1) Прогнозируют граничную глубину поиска.

2) Оценивают перспективность позиций игры с помощью эвристических функций. Для этого в каждой позиции игры формируется дерево возможных продолжений игры, имеющее определенную глубину, и с помощью эвристической оценочной функции вычисляются оценки концевых вершин такого дерева. Затем полученные оценки распространяются вверх по дереву и корневая вершина, соответствующая текущей позиции, получает оценку, позволяющую выяснить силу игрока в данной позиции. Например, при игре в шахматы современные программы просматривают возможные продолжения игры примерно на 10 ходов вперед. Основная идея такого оценивания заключается в том, что просмотр возможных продолжений игры из заданной позиции на определенную глубину позволяет точнее оценить перспективность того или иного хода.

Минимаксный метод.

В соответствии с минимаксным методом вместо полного просмотра дерева игры обследуется лишь его небольшая часть. В этом случае говорят, что дерево подвергается подрезке. Простейший способ подрезки – просмотр дерева игры на определенную глубину. Это означает, что процесс обследования заканчивается в вершинах, которые не являются терминальными (концевыми). Поэтому дерево поиска – только верхняя часть дерева игры.

Для оценки силы игрока в различных позициях поискового дерева применяются оценочные функции, причем, чем выше оценка в соответствующей позиции, тем больше шансов на выигрыш у игрока. Чем ниже оценка, тем выигрышнее позиция противника. Поэтому игрок стремится максимально увеличить выигрыш, а противник – минимизировать проигрыш.

Обычно в алгоритмах позиции игрока обозначают через max, а позиции противника – min. Различают 2 вида оценок: статические и динамические.

Статические оценки приписываются концевым вершинам дерева поиска и вычисляются на основе эмпирических правил. При игре в шахматы эти правила учитывают перевес фигур, контроль центра, подвижность фигур и т.д.

Динамические оценки получаются при распространении статических оценок вверх по дереву.

Метод, которым это достигается, называется минимаксным. Он заключается в следующем: для вершины, в которой ход выполняет игрок (max), выбирается наибольшая из оценок вершин нижнего уровня (то есть уровня min’a). Это оправдано, поскольку в этом случае игрок сделает для себя наиболее выгодный ход. Для вершины, в которой ход выполняет противник, выбирается наименьшая из оценок дочерних вершин, так как противник стремится сделать ход, наименее выгодный игроку.

На рисунке показан пример распространения статических оценок вверх по поисковому дереву в соответствии с указанным минимаксным принципом.

Из рисунка следует, что лучшим ходом max’a в вершине s будет ход s-d, а лучшим ходом min’a в вершине d будет ход d-l. Если обозначить статическую оценку в вершине p через h(p), а динамическую оценку через H(p), то формально оценки, приписываемые вершинам в соответствии с минимаксным принципом, можно записать так: H(p)=h(p), если p – терминальная вершина дерева поиска. H(p)=max i H(pi), если р – вершина с ходом max’a и H(p)=min i H(pi), если р – вершина с ходом min’a.

Многое в минимаксном методе зависит от оценочной функции. Если бы имелась абсолютно точная оценочная функция, то можно было гарантировать выигрыш. На практике для приближения минимаксной стратегии игры к гарантирующей приходится увеличивать глубину поиска. Поэтому разработаны подходы, позволяющие сократить объем перебора при обследовании дерева поиска. Один из них базируется на методе α-β-поиска.

α-β-поиск.

Минимаксный метод предполагает полное обследование дерева поиска. Чтобы получить оценку корневой вершины, совсем необязательно выполнять систематический обход дерева поиска. Рассмотрим пример α-β-поиска для случая, когда обход дерева выполняется сверху вниз и слева направо.

Дерево имеет следующий вид:

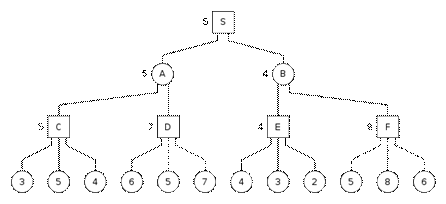
Процесс поиска начинается в позиции S и идет в направлении вершины C, для которой выбирается максимальная из оценок вершин-преемников позиции С: H(C)=5. Затем происходит возврат к вершине А и оценивание вершины D.

Для этого рассматривается первая вершина-преемник позиции D с оценкой 6, в этот момент обнаруживается, что игроку в вершине D гарантирована оценка не меньшая, чем 6. Этого достаточно, чтобы понять, что для противника позиция D хуже, чем С. Поэтому можно пренебречь вторым и третьим преемником позиции D и связать с вершиной D приближенную оценку 6.

Точно так же при обследовании правого поддерева вершины S игроку в позиции Е гарантируется оценка не меньшая, чем 4. Следовательно, противнику в позиции В гарантируется оценка не выше 4. Отсюда следует, что из позиции S лучше сделать ход S=>A, поэтому правое поддерево вершины В можно не анализировать.

Таким образом, сложность поиска уменьшилась за счет отсечения части дерева поиска. В α-β-поиске статическая оценка каждой терминальной вершины вычисляется сразу, как только такая вершина будет построена. Затем полученная оценка распространяется вверх по дереву и с каждой из родительских вершин связывается предположительно возвращаемая оценка (ПВО). При этом гарантируется, что для родительской вершины, в которой ход выполняет игрок (ее также называют α-вершиной) уточненная оценка, вычисляемая на последующих этапах, будет не ниже предположительно возвращаемой оценки.

Если же в родительской вершине ход выполняет противник (β-вершина), то гарантируется, что последующие оценки будут не выше ПВО. Это позволяет отказаться от построения некоторых вершин и сократить объем поиска. При этом используются следующие правила:

Правило 1. Если ПВО для β-вершины становится меньше или равной ПВО родительской вершины, вычисленной на предыдущем шаге, то нет необходимости строить дальше поддерево, начинающееся ниже этой β-вершины.

Правило 2. Если ПВО для α-вершины становится больше или равной ПВО родительской вершины, вычисленной на предыдущем шаге, то нет необходимости строить дальше поддерево, начинающееся ниже этой вершины.

Первое правило соответствует α-отсечению, а второе - β-отсечению. Для дерева поиска, изображенного в примере, ситуация α-отсечения имеет место при вычислении ПВО вершины вершины D: H(D)=7 > H(A)=5. Ситуация β-отсечения для вершины В: H(B)=4 < H(S)=5.

Результаты применения α-β-поиска зависят от порядка, в котором строятся дочерние вершины. В худшем случае α-β-поиск будет соответствовать минимаксному методу. Всегда первыми лучше рассматривать самые сильные ходы каждой из сторон. В этом случае α-β-алгоритм вычисляет статические оценки только в N вершинах, число которых равно числу терминальных вершин поискового дерева.

α-β-поиск позволяет увеличить глубину дерева поиска примерно в 2 раза по сравнению с минимаксным алгоритмом, что приводит к более сильной игре.