Оптимизационная модель задачи потребительского выбора. Уравнение Слуцкого

Для оценки различных ситуаций в сфере потребления применяются предельный спрос и предельная полезность денег по ценам (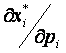 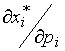и 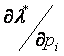) и доходу ( 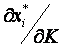и ).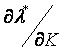

Их взаимосвязь определяется матричным уравнением:

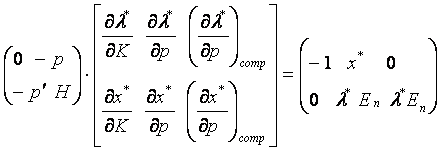(5.25)

Это уравнение (5.26) называется основным матричным уравнением теории потребления.

Матрица 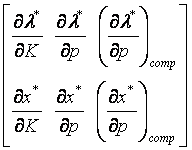называется матрицей сравнительной статики, а ее элементы - показателями сравнительной статики. Такое название объясняется тем, что эти показатели характеризуют чувствительность 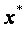и 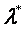к изменениям параметров 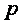и 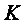путем сравнения положения оптимума в статике до и после того, как эти параметры изменились.

Левая часть уравнения (5.25) есть невырожденная матрица (ибо такой является Якобиан), а значить уравнение может быть разрешено относительно показателей сравнительной статики. Решение этого уравнения связано с понятием уравнения Слуцкого.

Основное матричное уравнение (5.25) можно записать следующим образом:

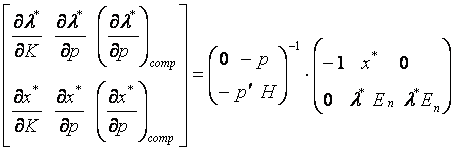(5.26)

Решение этой системы относительно показателей сравнительной статики по спросу имеет вид:

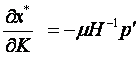	(5.27)
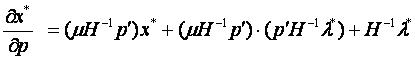	(5.28)
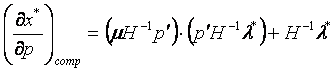	(5.29)

Здесь 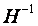- обратная матрица Гессе (матрица Гессе - матрица вторых производных: 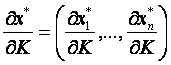), а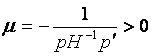

скалярная величина. Можно показать, что

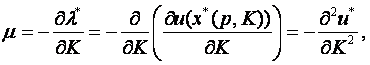
поэтому скаляр 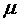можно интерпретировать как коэффициент убывания предельной полезности денег.

Сравнивая (5.29) и (5.28) замечаем, что

Сопоставляя это уравнение с (5.27), получаем,

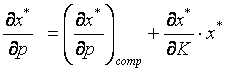(5.30)

Это равенство (5.30) называется уравнением Слуцкого. Это же уравнение называют основным уравнением теории ценности.

Уравнение Слуцкого, в частности, означает, что:

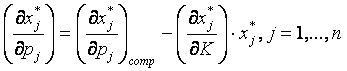(5.31)

Здесь производная 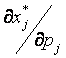называется влиянием на спрос (на j-й товар) изменения частной цены (цены j-го товара). Это равенство используют для характеристики типов товаров.

Определение. Товар вида j называется нормальным, если 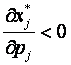; товаром Гиффина, если 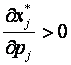; ценным, если 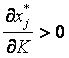; малоценным, если 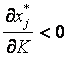. Два товара i и j являются взаимозаменяемыми, если 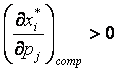взаимодополняемыми, если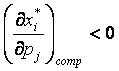

Из (5.31) следует, что

С учетом условия 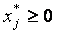приходим к следующим выводам:

а) если 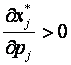, то обязательно ;

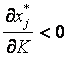б) если 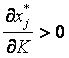, то обязательно .

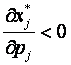Отсюда, товар Гиффина не может быть ценным, т.е. он обязательно малоценный.

Выводы:

Для вычисления предельного спроса и предельной полезности денег по ценам и доходу (то есть показателей сравнительной статики), которые применяются для оценки различных ситуаций в сфере потребления, выводится основное матричное уравнение теории полезности. Решая это уравнение получаем соотношение для показателей сравнительной статики, называемое основным уравнением теории ценности (уравнение Слуцкого). Оно отражает хорошо известное в экономической теории разделение общего эффекта (воздействие цены на спрос) на эффект замещения и на эффект дохода. С помощью уравнения Слуцкого можно классифицировать товары, анализировать их свойства и получить полезные для практики потребления выводы.