Экстремальные касательные напряжения

Прежде всего, укажем, что формулы 9.10 пригодны для плоского напряженного состояния, причем наклонные площадок, параллельны одной из главных осей. Действительно, из рис. 9.9 видно, что 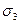не дает проекций на плоскость 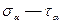. Таким образом формулы 9.10 остаются в силе.

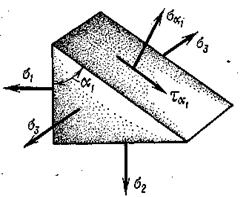
Рис. 9.9

Построим поочередно три круга Мора для семейства площадок параллельных осям 1.2.3 (Рис. 9.10).

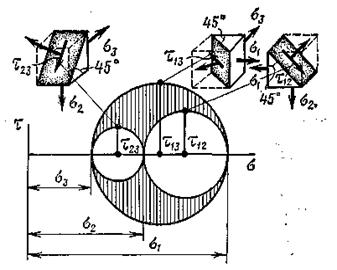
Рис. 9.10

Отмеченные точки являются вершинами кругов, которые соответствуют диагональным площадкам наклонным под углом 45⁰ к главным осям. В теории упругости доказывается, что для произвольно наклонных площадок (не параллельных ни одной из главных осей) нормальное и касательное напряжения определяются координатами точек заштрихованной области.

Как видно из рис. 9.10 максимальные касательные напряжения равны

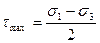(9.11)

Переход тела из упругого состояния в пластическое иногда связывают с величиной 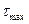, и поэтому наряду с главными напряжениями 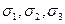оно является важной характеристикой напряженного состояния.