2014-02-02
744
Наиболее просто решается задача об изгибе бесконечно длинной балки, нагруженной одной сосредоточенной силой (Рис.2). Помимо непосредственного практического значения решение этой задачи позволит путем последовательных приближений рассчитывать и балки конечной длины.
Рис.2. Расчетная схема балки бесконечной длины.
Начало координат расположим в точке приложения силы Р. Определим постоянные А, В, С и D. Так как вся реакция основания, равная силе Р должна быть конечной величиной, то прогибы балки в точках, бесконечно удаленных от точки приложения силы, должны обращаться в нуль:
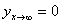| (5) |
При бесконечно больших значениях х два вторых слагаемых в правой части формулы (4) обращаются в нуль благодаря множителю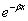 
, два же первых могут обратиться в нуль лишь пр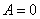и
и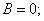 
таким образом,
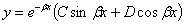| (6) |
Далее, по симметрии нагрузки и реакции основания, касательная к изогнутой оси в точке приложения силы должна идти параллельно оси абсцисс:
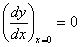
Дифференцируя (6), получаем:
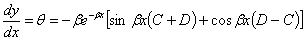
Подставляя в это выражение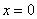 
и приравнивая результат нулю, находим:
D — С = 0 и C=D;
таким образом, уравнения будут:
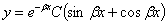| (7) |
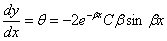| (8) |
Для определения последней постоянной С имеем еще одно уравнение: нам известна величина поперечной силы в начале координат.
Разрезав балку сечением в точке О справа от силы Р и рассматривая правую часть балки, видим, что поперечная сита в этом сечении равна реакции основания, действующей на правую половину балки со знаком минус; так как реакция направлена вверх (для правой половины) и вся реакция основания равна Р, значит, поперечная сила в сечении при х = 0 равна
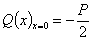
Но, с другой стороны
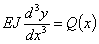| (9) |
Таким образом,
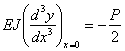| (10) |
Вычисляем, пользуясь (8),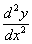 
и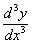 
:
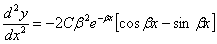| (11) |
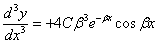| (12) |
Подставляя (12) в (10) и приравнивая х нулю, получаем:
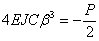и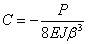 
Теперь значения у и ее производных получают вид
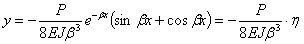
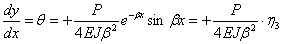
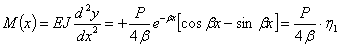
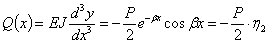
Таким образом, напряженное состояние и деформации балки на упругом основании всецело определяются нагрузкой и коэффициентом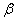 
, зависящим от соотношения жесткостей балки и упругого основания.
Лекция № 32. Энергетические методы расчета деформаций.
