Намагниченность. Магнитное поле в веществе

Степень намагничения магнетика характерезуют векторной величиной, называемой намагниченностью. Намагниченность – магнитный момент единицы объема магнетика.

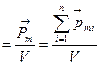, (4.9.9)

где 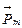- магнитный момент магнетика, численно равный сумме магнитных моментов отдельных молекул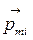. Магнетик в магнитном поле токов намагничивается и создает собственное магнитное поле. В результате вектор магнитной индукции поля:

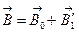, (4.9.10)

где 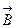₀ – вектор магнитной индукции поля, созданного в вакууме, 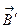- вектор магнитной индукции поля, созданного молекулярными токами. Индукция магнитного поля, созданного током в вакууме, связана с напряженностью 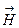, характеризующей магнитное поле макротоков, соотношением:

где m₀ – магнитная постоянная. Опыт показывает, что в однородных магнетиках целиком заполняющих пространство, где поле отлично от нуля, индукция 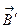может быть направлена как в ту же сторону, что и 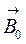(парамагнетики), так и в противоположную (диамагнетики). Свяжем вектор 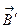с намагниченностью J. Установим эту связь для простого частного случая. Рассмотрим однородный магнетик в виде кругового цилиндра сечением S и длинной 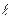, находящегося в однородном магнитном поле с индукцией 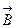₀. Магнетик намагнитится, что обусловлено наличием упорядоченных молекулярных токов. Плоскости молекулярных токов перпендикулярны вектору . 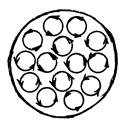В любом сечении цилиндра, перпендикулярном его оси, молекулярные токи соседних атомов во внутренних участках сечения направлены навстречу друг другу и созданные ими магнитные поля взаимно компенсируются (рис.22.2)

Нескомпенсированными остаются лишь поля, созданные токами текущими по боковой поверхности цилиндра. Эти токи аналогичны току в соленоиде, а потому внутри цилиндра они создают магнитное поле индукция которого 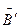равна:

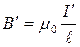, (4.9.11)

где 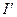- сила молекулярного тока, 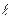- длинна цилиндра. Формула записана для одного витка.

С другой стороны,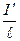- линейная плотность тока. Магнитный момент этого тока:

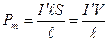, (4.9.12)

где V – объем магнетика. Намагниченность магнетика:

J 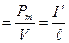. (4.9.13)

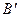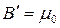Сравнение (4.9.11) с (4.9.13) дает связь с J:

J

или в векторной форме

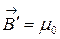J. (4.9.14)

Найдем магнитную индукцию результирующего поля

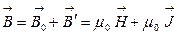(4.9.15)

или

.

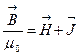Из опыта известно, что в несильных полях намагниченность прямо пропорциональна напряженности поля заданных внешних токов (намагничивающего поля.):

= æ 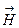, (4.9.16)

где æ - безразмерная величина, характеризующая данный магнетик, называемая магнитной восприимчивостью вещества. Итак,

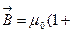æ)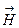, (4.9.17)

откуда: 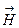= 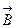/m₀(1+ æ). (4.9.18)

Безразмерную величину (1 + æ) принято обозначать одной буквой m.

1 + æ = m (4.9.19)

и называть магнитной проницаемостью среды. С учетом всего сказанного:

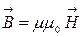. (4.9.20)

Полученные формулы справедливы лишь для однородных магнетиков. Магнитная восприимчивость æ - физическая величина, характеризующая способность вещества изменять свой магнитный момент под действием магнитного поля. Если в магнитном поле нет вещества, то J = 0, т.е. для вакуума æ = 0. В вакууме m = m₀, поэтому магнитная постоянная m₀ называется магнитной проницаемостью вакуума.

Магнетики, у которых æ < 0 и мала по обсалютной величине называются диамагнетиками. Для них m <1.

Магнетики, у которых æ >0 (m > 1) и также мала по величине, называются парамагнетиками. И еще один класс магнетиков – ферромагнетики, для которых æ > 0 и достигает очень больших значений. Если для диа- и парамагнетиков æ =const, то у ферромагнетиков магнитная воспиримчивость является функцией напряженности поля æ =¦(Н). Вектор намагничения J у пара- и ферромагнетиков совпадает по направлению с напряженностью магнитного поля, у диамгнетиков он направлен в противоположную сторону.