Задачи обучения

(1) Апросимакция функции.

Рассмотрим не линейнные отображения типа «вход-выход» заданные соотношение 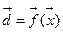; (5) где, вектор d-выход, вектор x- вход.

Векторная функция 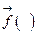считается неизвестной.

Для аппроксимакции 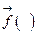возьмем множество примеров:

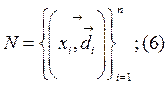
Нейронная сеть выполняет роль аппроксиматора. К структуре нейронной сети предъявляются следующие требования, 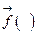- которая описывает выражение векторного отображения должна быть близка в функции 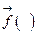в смысле эвклидовой нормы на множестве всех входных векторов .

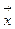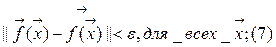
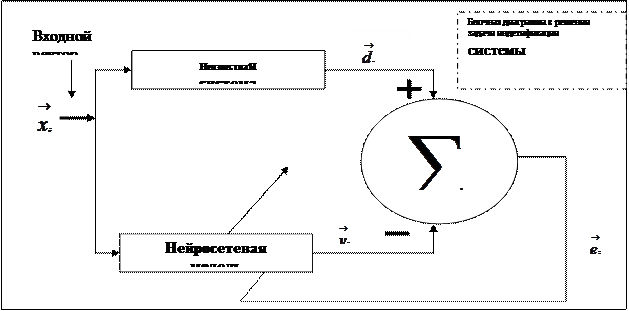
где «эпсилонт», некоторое малое положительно число. Когда количество n элементов обучающего множества достаточно велико и НС содержит достаточное количество свободных параметров(синоптических весов), то ошибка апросимакции «епсилонт» может быть достаточно малой. Постановка большого количества задач моделирования, идентификации систем, обработки сигналов, может быть сведена к апросикционнаму представлению. Рассмотрим задачу идентификации систем, допустим, что формула 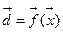описывает соотношение в неизвестной системе имеющий несколько входов и выходов, которая инвариантна во времени(не меняется с течением времени), тогда множество примеров 6 можно использовать для обучения нейронной сети представляющей модель этой системы.

пусть 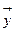выход нейронной сети соответствующий вектору . Разность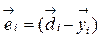

Он используется для корректировки свободных параметров нейронной сети с целью минимизации среднекравадратичной ошибки - Сумма квадратов разности между выходами неизвестной системы нейронной сети, вычисляемой на множестве всех примеров, т.е. в статистическом смысле.