Основные понятия и определения. Глава 1. Дифференциальные уравнения первого порядка

Глава 1. Дифференциальные уравнения первого порядка

Дифференциальные уравнения обычно используются для построения математических моделей процессов, параметры которых изменяются с течением времени. В качестве простейшего примера рассмотрим математическую модель движения автомобиля по прямолинейному шоссе, считая, что в каждый момент времени 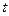скорость автомобиля выражается известной величиной 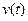. Если принять шоссе за ось 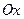, то положение автомобиля будет определяться одной координатой 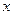. Используя механический смысл производной, получаем дифференциальное уравнение

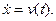
Полученное уравнение позволяет найти закон движения автомобиля, т.е. зависимость его координаты от времени.

Искомой величиной в любом дифференциальном уравнении является функция. Также в дифференциальное уравнение входит аргумент этой функции и её производные различных порядков. Дифференциальное уравнение называется обыкновенным, если оно содержит только обыкновенные производные от искомой функции; таким образом, в обыкновенном дифференциальном уравнении искомая функция зависит только от одного аргумента. Порядком обыкновенного дифференциального уравнения называется порядок старшей производной, входящей в это уравнение. Таким образом, обыкновенным дифференциальным уравнением первого порядка называется соотношение, связывающее искомую функцию, её аргумент и первую производную от искомой функции. Такое соотношение может быть записано следующим образом

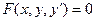. (1)

Здесь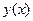– искомая функция,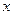- её аргумент и .

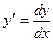Если уравнение (1) можно переписать в виде

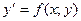, (2)

то уравнение (2) называется уравнением, разрешённым относительно производной или уравнением в нормальной форме.

В некоторых случаях возникает необходимость использовать уравнение

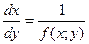, (3)

которое называется перевёрнутым уравнением.

Вместо двух уравнений (2) и (3) можно использовать одно уравнение, записанное в форме

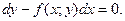(4)

Уравнение (4) содержит не производную от искомой функции, а дифференциалы этой функции и её аргумента. Это частный случай уравнения, записанного в дифференциалах. В общем случае уравнение в дифференциалах имеет вид

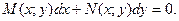(5)

В уравнения (4) и (5) переменные 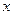и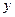входят равноправно. Запись уравнения в виде (5) показывает, что при решении дифференциального уравнения первого порядка любую величину 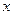или 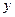можно рассматривать в качестве аргумента, а другую – принять за искомую функцию.

Наконец, ещё одной формой записи дифференциального уравнения первого порядка является симметрическая форма. Уравнение в симметрической форме выглядит так:

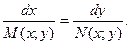(6)

В это уравнение переменные 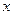и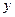также входят равноправно.

Перейдём к определению решения дифференциального уравнения первого порядка и формам записи решения. Будем рассматривать уравнение в виде (2) и будем считать, что функция 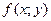определена на некотором множестве 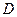на плоскости переменных 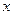и.

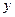Решением дифференциального уравнения первого порядка (2) на интервале называется функция 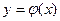, которая определена и дифференцируема во всех точках указанного интервала и при подстановке в уравнение (2) превращает его в тождество на этом интервале. При этом решения уравнения (3) также считаются решениями уравнения (2).

Пример 1. Проверим, что функция 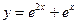является решением уравнения 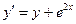на всей вещественной оси. Действительно, данная функция определена и дифференцируема во всех точках вещественной оси и после подстановки этой функции в уравнение получается тождество, верное на всей оси: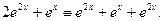

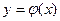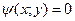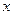Если решение уравнения получено в виде , то говорят, что решение записано в явной форме. Однако решение дифференциального уравнения не всегда записывается в явной форме. Соотношение называется решением уравнения (2) в неявной форме, если оно определяет как неявную функцию и эта функция является решением уравнения (2). Для того, чтобы убедиться, что равенство 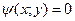- действительно неявная форма записи решения, нужно продифференцировать это соотношение полным образом по 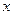и подставить вместо 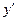правую часть уравнения (2):

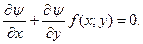(7)

Если равенство нулю в формуле (7) выполнится в силу соотношения 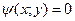, то действительно решение уравнения, записанное в неявной форме.

Пример 2. Пусть дано уравнение 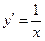и соотношение 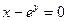. Дифференцируя, как указано выше, получаем 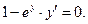Подставляя вместо 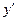величину 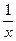, убеждаемся, что 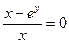, в силу того, что 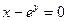. Значит, равенство 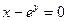- неявная форма записи решения.

Решение уравнения (2) может быть записано также и в параметрической форме, то есть в виде двух соотношени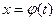й и 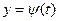которые на некотором интервале дают тождество

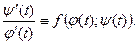
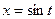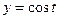Пример 3. Проверим, что равенства и определяют решение уравнения 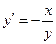на интервале 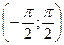. Действительно, 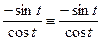на указанном интервале.

Если рассматривать и как прямоугольные координаты на плоскости, то решение уравнения (2) может быть изображено на этой плоскости в виде некоторой кривой. График решения уравнения на плоскости называется интегральной кривой уравнения (2).

Рассмотрим простейшее дифференциальное уравнени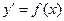е , где 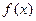- заданная функция, непрерывная на некотором интервале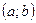. Известно, что тогда

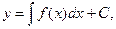(8)

Здесь 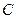- постоянная интегрирования. Из формулы (8) видно, что дифференциальное уравнение 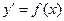имеет не одно решение, а семейство решений, зависящее от одной произвольной постоянной 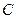. Далее будет показано, что любое дифференциальное уравнение первого порядка при определённых условиях также имеет семейство решений, зависящее от одной произвольной постоянной 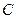, которая изменяется на некотором множестве 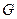. Такое семейство называется общим решением уравнения (2) и записывается в виде

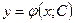. (9)

Подставляя в формулу (9) фиксированные значения константы 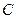, мы получим некоторые решения уравнения (2), которые называются частными решениями этого уравнения. Таким образом, общее решение уравнения состоит из частных его решений. Однако при некоторых условиях уравнение (2) может иметь решения, которые не включаются в общее решение ни при каких фиксированных значениях 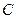, в том числе при значениях 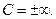Такие решения уравнения (2) называются особыми решениями.

Пример 4. Рассмотрим уравнени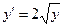е , где 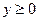. Его общее решение задаётся формулой 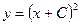, 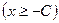. Однако данное уравнение очевидно имеет также решение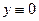, которое не входит в семейство ни при каких постоянных значениях 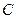. Итак, 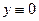- особое решение уравнения.

В следующих параграфах будут приведены строгие определения общего, частного и особого решений.

Выясним, как составить дифференциальное уравнение, которому удовлетворяет заданное семейство кривых. Пусть это семейство определяется формулой 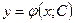. Для получения дифференциального уравнения, нужно продифференцировать данное соотношение по 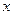и исключить из полученных равенств константу .

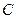Пример 5. Дано семейство полупрямых 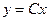; 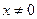. Отсюда 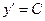, тогда 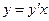или, окончательно, 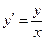. Искомое уравнение получено.

Задача решения или интегрирования дифференциального уравнения состоит в нахождении его общего решения или некоторого конкретного решения, удовлетворяющего дополнительно заданным условиям.