III. Какие основные типы задач с параметрами?
II. Что означает «решить задачу с параметром»?
Это зависит от вопроса в задаче.
Если, например, требуется решить уравнение, неравенство, их систему или совокупность, то это означает предъявить обоснованный ответ либо для любого значения параметра, либо для значения параметра, принадлежащего заранее оговоренному множеству.
Если же требуется найти значения параметра, при которых множество решений уравнения, неравенства и т. д. удовлетворяет объявленному условию, то, очевидно, решение задачи и состоит в поиске указанных значений параметра.
Тип 1. Уравнения, неравенства, их системы и совокупности, которые необходимо решить либо для любого значения параметра (параметров), либо для значений параметра, принадлежащих заранее оговоренному множеству.
Тип 2. Уравнения, неравенства, их системы и совокупности, для которых требуется определить количество решений в зависимости от значения параметра (параметров).
Тип 3. Уравнения, неравенства, их системы и совокупности, для которых требуется найти все те значения параметра, при которых указанные уравнения, неравенства, их системы и совокупности имеют заданное число решений (в частности, не имеют или имеют бесконечное множество решений).
Тип 4. Уравнения, неравенства, их системы и совокупности, для которых при искомых значениях параметра множество решений удовлетворяет заданным условиям в области определения.
Способ I - аналитический. Это способ так называемого прямого решения, повторяющего стандартные процедуры нахождения ответа в задачах без параметра. Иногда говорят, что это способ силового, в хорошем смысле «наглого» решения.
Комментарий. По мнению авторов, аналитический способ решения задач с параметром есть самый трудный способ, требующий высокой грамотности и наибольших усилий по овладению им.
Способ II - графический. В зависимости от задачи (с переменной x и параметром a) рассматриваются графики или в координатной плоскости (x; y), или в координатной плоскости (x; a).
Комментарий. Исключительная наглядность и красота графического способа решения задач с параметром настолько увлекает изучающих тему «Задачи с параметром», что они начинают игнорировать другие способы решения, забывая общеизвестный факт: для любого класса задач их авторы могут сформулировать такую, которая блестяще решается данным способом и с колоссальными трудностями остальными способами. Поэтому на начальной стадии изучения опасно начинать с графических приемов решения задач с параметром.
Способ III - решение относительно параметра. При решении этим способом переменные x и a принимаются равноправными и выбирается та переменная, относительно которой аналитическое решение признается более простым. После естественных упрощений возвращаемся к исходному смыслу переменных x и a и заканчиваем решение.
Перейдем теперь к демонстрации указанных способов решения задач с параметром.
Задача 1. Для всех действительных значений параметра a решите уравнение
x3–(2–a)x2–ax–a(a–2)=0.
Решение:
1) Исходное кубическое по x уравнение является квадратным относительно a. Поэтому, считая переменную x параметром, перепишем это уравнение в виде стандартного квадратного уравнения относительно a, опуская промежуточные шаги по раскрытию скобок и перегруппировке: a 2–(x2–x+2) a – x3 + 2x2 = 0.
2) Поскольку x2–x+2=x2+(2–x) и –x3+2x2=x2(2–x), то по обратной теореме Виета
a 1=x2, a 2=2–x.
3) Поэтому исходное уравнение равносильно совокупности уравнений a =x2 и a =2–x.
Первое уравнение преобразуется к виду x2= a, откуда
(1): при a <0 решений нет;
(2): при a =0 единственное решение x=0; при a >0 два решения
(3): 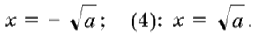
Второе уравнение совокупности имеет единственное решение (5): x=2 – a для любого значения параметра a.
4) Изображаем ось параметра a и отмечаем на ней граничные значения параметра, которые фигурируют в ответах к каждому уравнению совокупности. Все найденные решения уравнений для тех значений параметра a, при которых хотя бы одно решение существует, выписываем в таблице слева (последовательно сверху вниз). Сплошной линией, параллельной оси параметра, указываем те промежутки значений параметра, при которых полученное решение существует. Заметим, что концы промежутков изображаются «светлыми» точками в случае, когда соответствующее решение не существует, а «темными» точками — в противном случае.
Таблица 1
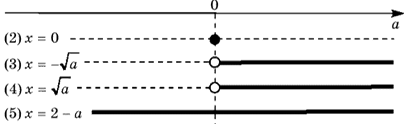
Данная развертка позволяет легко найти все решения исходного уравнения для любого действительного значения параметра: x=2–a при a <0; x=0 или x=2 при a =0;  или
или 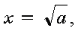 или x=2– a при a >0.
или x=2– a при a >0.
5) Формирование ответа. Например, при a = 1 равенства 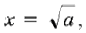 и x = 2 – a определяют одно и то же значение переменной x=1, а при a =4 равенства
и x = 2 – a определяют одно и то же значение переменной x=1, а при a =4 равенства 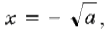 и x=2 – a аналогично определяют одно значение x=–2.
и x=2 – a аналогично определяют одно значение x=–2.
Полученные равенства (2)–(5) могут при некоторых значениях параметра a определять одно и то же значение переменной x. Найдем указанные значения параметра. Поскольку значения 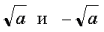 – различны для всех a >0, осталось выяснить, при каких значениях a выполняются равенства
– различны для всех a >0, осталось выяснить, при каких значениях a выполняются равенства 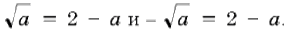 Пусть
Пусть 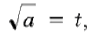 тогда первое уравнение приводится к виду t2+t–2=0, откуда t=1 и t=–2 (не подходит, так как
тогда первое уравнение приводится к виду t2+t–2=0, откуда t=1 и t=–2 (не подходит, так как 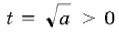 при a > 0), т. е.
при a > 0), т. е.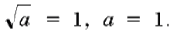 . Аналогично решая второе уравнение, находим a =4.
. Аналогично решая второе уравнение, находим a =4.
Таблица 2
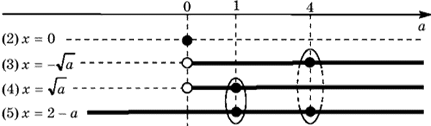
Полученный результат в таблице 2 проиллюстрирован следующим образом: линии равенства (4) и (5) «сливаются» при a =1, линии (3) и (5) «сливаются» при a =4.
Используя таблицу 2, легко сформулировать окончательный ответ задачи.
Ответ: x=2– a при a <0; x1=0, x2=2 при a =0; 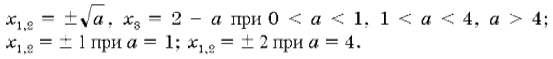
Задача 2. Для всех действительных значений параметра a найдите число различных корней уравнения (a–x2)(a+x–2)=0.
Решение:
1) Исходное уравнение равносильно совокупности a –x2=0 или a +x–2=0.
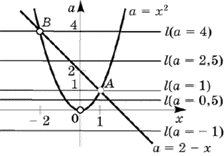
2) Поэтому построение искомого множества точек — графика уравнения — сводится к построению графиков a = x2 и a =2–x (рис. 1).
 2014-02-02
2014-02-02 8181
8181