2014-02-02
887
Метод описания колебаний путем построения траектории тражения системы в плоскости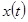 
-
.
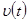Рассмотрим еще один наглядный способ графического представления произвольных (не только гармонических) колебаний. Пусть закон колебательного движения описывается функцией 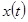, которая обязательно является периодической. По известному закону движения можно определить зависимость скорости от времени, как производную от координаты 
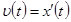. Введем на плоскости систему декартовую систему координат, вдоль одной из осей которой будем откладывать координату точки, а вдоль другой − ее скорость. Введенная таким образом система называется фазовой плоскостью. Две функции x(t) и v(t) в любой момент времени определяют на этой плоскости некоторую точку, а геометрическое место этих точек образует некоторую непрерывную линию, которая называется фазовой траекторией или фазовым портретом.
Траектория движения точки в плоскости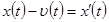 
называется фазовым портретом.
Особенно просто выглядит фазовая траектория гармонического колебания, при котором координата и скорость описываются функциями
, 
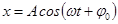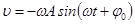
Из этих уравнений следует, что уравнение фазовой траектории можно записать в виде:
,
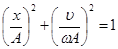которое является уравнением эллипса с полуосям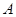и 
и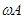 
.
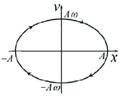С помощью фазовой диаграммы легко качественно (не проводя числовых расчетов) анализировать характер колебания. Например, для затухающих колебаний фазовая диаграмма будет представлять собой скручивающуюся спираль, при наличии усиления – спираль будет раскручиваться.
