2014-02-02
1156
Дополнительный код
Для получения дополнительного кода отрицательного числа можно использовать следющий алгоритм:
1. Модуль числа записать прямым кодом в n двоичных разрядах;
2. Получить обратный код числа; для этого значения всех бит инвертировать (все единицы заменить на нули и все нули заменить на единицы);
3. К полученному обратному коду прибавить единицу.
Пример 2.3. Записать дополнительный код отрицательного числа –2002 для 16-ти разрядного компьютерного представления.
| Прямой код | |-200210| | 1 0000111110100102 |
| Обратный код | инвертирование | 1 1111000001011012 |
| прибавление единицы | 1 1111000001011012 + 00000000000000012 | |
| Дополнительный код | 1 1111000001011102 |
Пример 2.4. Выполнить арифметическое действие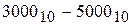 
в машинном коде.
Решение. Представим положительное число в прямом, а отрицательное число в дополнительном коде:
| Десятичное число | Прямой код | Обратный код | Дополнительный код | ||
| 0 000101110111000 | |||||
| -5000 | 1 001001110001000 | 1 110110001110111 | 1 110110001110111 + 000000000000001 1 110110001111000 | ||
| Сложим прямой код положительного числа с дополнительным кодом отрицательного числа. Получим результат в дополнительном коде: | |||||
| 3000-5000 | 0 000101110111000 + 1 110110001111000 1 111100000110000 | ||||
Ответ получен в дополнительном коде, так как в знаковом разряде 1. Переведем полученный дополнительный код в десятичное число:
|
|
|
1. Инвертируем дополнительный код: 0000011111001111;
2. Прибавим к полученному коду 1 и получим модуль отрицательного числа:
| + 0000000000000001 |
3. Переведем в десятичное число и припишем знак отрицательного числа: -2000.
Положительные числа в дополнительном коде записываются так же, как и в прямом. Нуль в дополнительном коде имеет единственное представление:
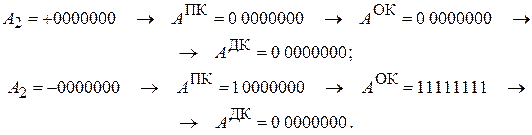
Обратный и дополнительный коды с точки зрения простоты выполнения операций над числами равноценны. Однако операции с удвоенной разрядностью в дополнительном коде выполняются проще, поэтому его чаще используют.
