2014-02-02
849
Логические выражения называются равносильными, если их истинностные значения совпадают при любых значениях, входящих в них логических переменных.
В алгебре логики имеется ряд законов, позволяющих производить равносильные преобразования логических выражений. К ним относятся:
Таблица 2.2
| № п/п | Название закона | Запись закона |
| Законы идемпотентности (одинаковости) | A + A = A; A×A = A. | |
| Законы коммутативности (переместительный) | А + B = B + A; A×B = B×A. | |
| Законы ассоциативности (сочетательный) | (A + B) + C = A + (B + C); (A×B) ×C = A× (B×C) | |
| Законы дистрибутивности (распределительный) | (A + B) ×C = (A×C) + (B×C) (A×B) + C = (A + C) × (B + C) | |
| Закон двойного отрицания: | 
| |
| Законы де Моргана (законы общей инверсии) |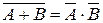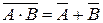 
| |
| Законы поглощения | A + (A×B) = A A×(A + B) = A | |
| Законы, определяющие действия с логическими константами 0 и 1 |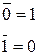 
Законы исключения констант:
A + 1 = 1
A + 0 = A
A×1 = A,
A×0 = 0
Закон противоречия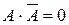
Закон исключения третьего
| |
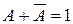| Законы склеивания (исключения) |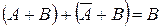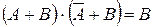 
| |
| Закон Блейка-Порецкого |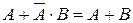 
| |
| Закон свертки логического выражения |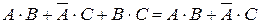 
| |
| Закон контрапозиции | (A Û B) = (BÛ A) |
|
|
|
