Приложения формул Тейлора и Маклорена.
Формулы Тейлора и Маклорена имеют широчайшее применение, как для приближенного вычисления значений целого ряда табулированных функций таких, например, как 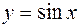 ,
, 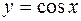 ,
,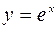 и др., так и для замены сложных функций при решении практических задач многочленами.
и др., так и для замены сложных функций при решении практических задач многочленами.
В качестве примера приложения формулы Маклорена, определим количество членов в разложении функции 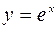 по указанной формуле для вычисления ее значения с точностью до 0.001 при любом x из промежутка
по указанной формуле для вычисления ее значения с точностью до 0.001 при любом x из промежутка
[-1,1].
Поскольку 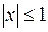 , то в остаточном члене
, то в остаточном члене  величина
величина 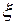 удовлетворяет неравенству:
удовлетворяет неравенству: 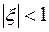 . Следовательно,
. Следовательно,
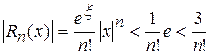 .
.
Очевидно, что если мы заменим на промежутке [-1,1] функцию 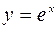 соответствующим многочленом Тейлора, то значения этого многочлена на указанном промежутке будут отличаться от соответствующих значений функции на величину меньшую, чем
соответствующим многочленом Тейлора, то значения этого многочлена на указанном промежутке будут отличаться от соответствующих значений функции на величину меньшую, чем 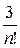 . Выбирая n из условия
. Выбирая n из условия 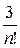 <0.001, мы получим, что
<0.001, мы получим, что 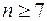 , поскольку (
, поскольку (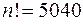 ).
).
Отметим, что формул Тейлора может использоваться и при вычислении пределов.
Вопросы для самоконтроля.
1. Написать формулы Тейлора и Маклорена для случаев n=2, n=3 и n=5.
Задачи для самоконтроля.
1. Разложить по формуле Тейлора функцию 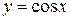 в точке
в точке 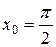 для случая n=4.
для случая n=4.
2. Разложить по степеням 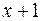 многочлен
многочлен 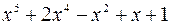 .
.
3. Написать формулу Тейлора для функции 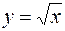 при
при 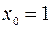 и
и 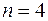 .
.
Задача 1. Воспользовавшись формулой Тейлора, разложить функцию  по степеням бинома
по степеням бинома  до четвертой степени включительно (остаточный член должен иметь сомножитель
до четвертой степени включительно (остаточный член должен иметь сомножитель 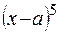 ) и вычислить приближенное значение функции в точке
) и вычислить приближенное значение функции в точке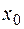 , отбросив остаточный член.
, отбросив остаточный член.
(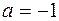 ;
; 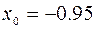 ).
).
Решение:Найдем значение функции 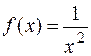 и ее производных до четвертого порядка включительно в точке
и ее производных до четвертого порядка включительно в точке 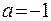 .
.
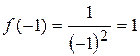 ;
; 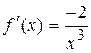 ;
; 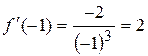 ;
;
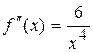 ;
; 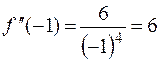 ;
;
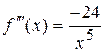 ;
; 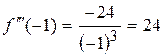 .
.
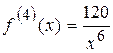 ;
;  .
.
Для того чтобы записать остаточный член формулы Тейлора, необходимо определить пятую производную функции 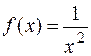 в точке
в точке 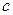 :
:
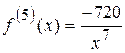 ;
; 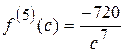 .
.
Тогда
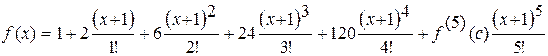 .
.
 2014-02-02
2014-02-02 1753
1753