Волгодонск
Конспект лекции №6
по теме:
«Асимптоты кривых. Общая схема исследования функции»
 |
Определение: Прямая l называется асимптотой графика функции 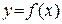 , если расстояние от точки М на графике до прямой l стремится к нулю при удалении точки М по графику функции от начала координат.
, если расстояние от точки М на графике до прямой l стремится к нулю при удалении точки М по графику функции от начала координат.
Асимптоты бывают вертикальные, горизонтальные, наклонные.
Вертикальной асимптотой называется прямая x=a, если 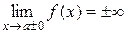 .
.
Находят вертикальную асимптоту по точкам разрыва второго рода (бесконечный разрыв).
Наклонной асимптотой называется асимптота, уравнение которой имеет вид:  .
.
Оказывается, что если  является асимптотой, то
является асимптотой, то 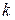 и
и 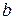 в уравнении определяются следующим образом
в уравнении определяются следующим образом 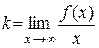 ,
, 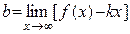 .
.
Доказательство:
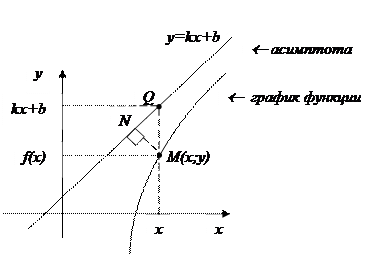
По определению асимптоты: если ОМ 
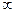 , то |MN|
, то |MN|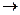 0.
0.
Þ |MQ|→0 при x→±∞, т.к. 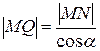 .
.
По чертежу:  .
.
Перейдем к пределу при x→±∞:
 (*)
(*)
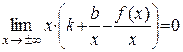
Þ 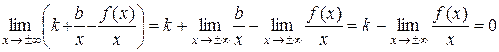 .
.
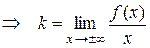 .
.
Из (*) Þ 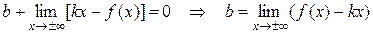 .
.
Ч.т.д.
Замечание 1: Чтобы у кривой были наклонные асимптоты, нужно, чтобы соответствующие пределы в определении k и b были конечными, причем предел при x→+∞ и предел при x→-∞ нужно вычислять отдельно.
Замечание 2: Если k=0, то y=b. Наклонная асимптота в этом случае называется горизонтальной.
Замечание 3: Кривая никогда не пересекает вертикальную асимптоту, а горизонтальные и наклонные асимптоты кривая может пересекать и даже бесконечное число раз.
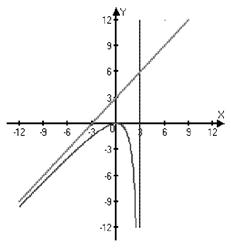
Пример: Найти асимптоты графика функции 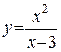 .
.
D(y): x¹3.
Þ x=3 – точка разрыва.
 — вертикальная асимптота.
— вертикальная асимптота.
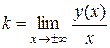 =
=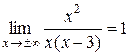 ;
;
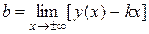 =
=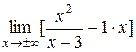 = =
= =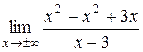 =3 Þ
=3 Þ 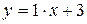 .
.
Þ 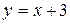 — наклонная асимптота.
— наклонная асимптота.
 2014-02-02
2014-02-02 1246
1246







