Вопросы для самопроверки. Область определения этой функции. Необходимо исследовать поведение функции в точке

Рис 3.2

Рис. 3.1

б) .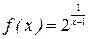

Область определения этой функции 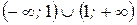.Необходимо исследовать поведение функции в точке 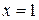, так как в ней функция не определена. Найдем левосторонний и правосторонний пределы функции в этой точке:

(здесь положил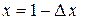и и ).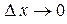

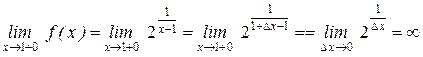
(положил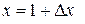и и ).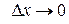

Таким образом, левосторонний предел функции равен 0 и конечен, а правосторонний предел функции равен бесконечности. Следовательно, точка 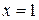есть точка разрыва 2-го рода.

Кроме того, найдем предел функции при х ® ± ¥.

,

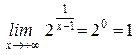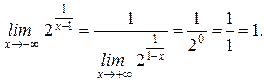
Тогда прямая 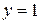является горизонтальной асимптотой.

Найдем значения функции в нескольких точках:

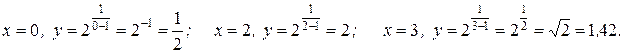Построим график функции (рис.3.2).

1. Сформулируйте определение непрерывности функции в точке и на интервале.

2. Сформулируйте основные свойства функций, непрерывных на интервале, и дайте геометрическое истолкование этим свойствам.

3. Что называется точкой разрыва функции? Приведите примеры.

4. Дайте определение точки разрыва 1-го рода и точки разрыва 2-го рода. Приведите примеры.