Для исследования взаимосвязи качественных альтернативных признаков, принимающих только 2 взаимоисключающих значения, используется коэффициент ассоциации и контингенции. При расчете этих коэффициентов составляется т.н. таблица 4-х камней, а сами коэффициенты рассчитываются по формуле:
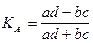
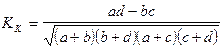
| Группы по признаку Y | Группы по признаку X | + | - | Итого: |
| + | a | b | a+b | |
| - | c | d | c+d | |
| Итого: | a+c | c+d | a+b+c+d |
Если коэффициент ассоциации ³ 0,5, а коэффициент контингенции ³ 0,3, то можно сделать вывод о наличии существенной зависимости между изучаемыми признаками.
Если признаки имеют 3 или более градаций, то для изучения взаимосвязей используются коэффициенты Пирсена и Чупрова. Они рассчитываются по формулам:
С - коэффициент Пирсена
К - коэффициент Чупрова
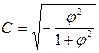
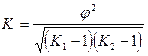
j - показатель взаимной сопряженности
K - число значений (групп) первого признака
K1 - число значений (групп) второго признака
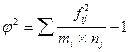
fij - частоты соответствующих клеток таблицы
mi - столбцы таблицы
nj - строки
Для расчета коэффициентов Пирсена и Чупрова составляется вспомогательная таблица:
| Группа признака Y | Группа признака X | ... | i | Итого: | ||
| f11 | f12 | ... | f1i | n1 | ||
| f21 | f22 | ... | f2i | n2 | ||
| ... | ... | ... | ... | ... | ... | |
| j | fji | fj2 | ... | fji | nj | |
| Итого: | m1 | m2 | ... | mi | SSminj |
При ранжировании качественных признаков с целью изучения их взаимосвязи используется коэффициент корреляции Кэндалла.
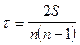
n - число наблюдений
S - сумма разностей между числом последовательностей и числом инвервий по второму признаку.
S=P+Q
P - сумма значений рангов, следующих за данными и превышающих его величину
Q - сумма значений рангов, следующих за данными и меньших его величины (учитывается со знаком «-»).
При наличии связанных рангов формула коэффициента Кендалла будет следующей:
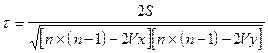
Vx и Vy определяются отдельно для рангов X и Y по формуле:
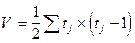
 2014-02-02
2014-02-02 453
453








