Обнаружение

Существует несколько признаков, по которым может быть установлено наличие мультиколлинеарности.

Во-первых, анализ корреляционной матрицы парных коэффициентов корреляции:

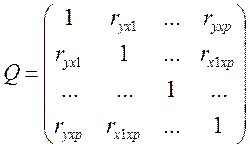
- если имеются пары переменных, имеющих высокие коэффициенты корреляции (> 0,75 – 0,8), говорят о мультиколлинеарности между ними;

- если факторы некоррелированы, то det Q = 1, если полная корреляция, то det Q = 0.

Можно проверить Н₀: det Q = 1; используя статистический критерий 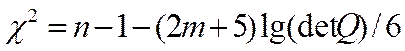, где n – число наблюдений, m = р+1.

Если 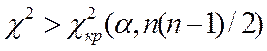, то Н₀ отвергается, и мультиколлинеарность доказана.

Во-вторых, определяют множественные коэффициенты детерминации одной из объясняющих переменных и некоторой группой других. Наличие высокого R² (> 0,6) свидетельствует о мультиколлинеарности.

В третьих, близость к нулю 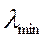- минимального собственного значения матрицы Х^ТХ (т.е. решения уравнения 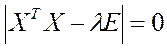) свидетельствует о близости к нулю и det(X^TX) и, следовательно, о мультиколлинеарности.

В-четвертых, высокие частные коэффициенты корреляции.

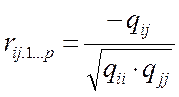, где 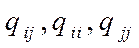- алгебраические дополнения элементов 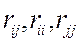матрицы выборочных коэффициентов корреляции. Коэффициенты частной корреляции более высоких порядков можно определить через коэффициенты частной корреляции более низких порядков по рекуррентной формуле:

.

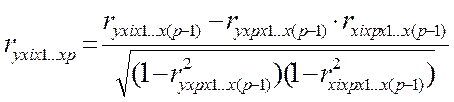В-пятых, о присутствии мультиколлинеарности говорят некоторые внешние признаки построенной модели, являющиеся её следствиями. К ним следует отнести такие:

· некоторые из оценок имеют неправильные с точки зрения экономической теории знаки или неоправданно большие по абсолютной величине значения;

· небольшое изменение исходных статистических данных (добавление или изъятие некоторых наблюдений) приводит к существенному изменению оценок коэффициентов модели, вплоть до изменения их знаков;

· большинство или даже все оценки коэффициентов регрессии оказываются статистически незначимыми по t-критерию, в то время как модель в целом является значимой по F-критерию.

Существует и ряд других методов определения мультиколлинеарности.

Если основная задача модели – прогноз будущих значений зависимой переменной, то при достаточно большом коэффициенте детерминации R² (> 0,9) наличие мультиколлинеарности обычно не сказывается на прогнозных качествах модели. Это утверждение будет обоснованным, если и в будущем между коррелированными переменными сохранятся те же соотношения.

Если целью исследования является определение степени влияния каждой из объясняющих переменных на зависимую переменную, то наличие мультиколлинеарности, приводящее к увеличению стандартных ошибок, скорее всего, исказит истинные зависимости между переменными. В этой ситуации мультиколлинеарность является серьезной проблемой.