Способы устранения мультиколлинеарности. Отбор наиболее существенных факторов

Единого метода устранения мультиколлинеарности, годного в любом случае, не существует. Это связано с тем, что причины и последствия мультиколлинеарности неоднозначны и во многом зависят от результатов выборки. Все методы, которые могут быть использованы, делятся на две категории: к первой относятся попытки повысить степень выполнения условий Гаусса-Маркова, ко второй – использование внешней информации.

1. Так как проблема практически всегда возникает в регрессиях по временным рядам, то можно увеличить число наблюдений (от ежегодных к поквартальным). Однако надо не забывать об усилении автокорреляции и ошибок измерения.

2. При перекрестных данных можно увеличить дисперсию наблюдений независимых переменных в выборке.

3. Отбор наиболее существенных факторов. Можно использовать процедуры пошагового включения или исключения факторов. Например, процедура пошагового отбора состоит в следующем:

а) строят уравнение регрессии с полным набором факторов;

б) определяют матрицы парных и частных коэффициентов корреляции;

в) отбирают фактор с наименьшей (отбор) или наибольшей (включение) величиной коэффициента частной корреляции по t-критерию: , r – должен быть существенным для включения и несущественным для исключения;

г) строят новое уравнение регрессии:

- при отсеве – пока все факторы не будут существенно отличны от нуля;

- при включении – пока увеличивается .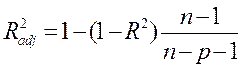

4. Переход от несмещенных оценок к смещенным, т.е.

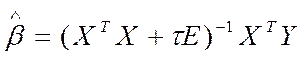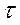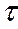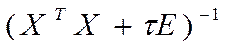, где - некоторое положительное число (=0,10,4). Таким образом, - невырожденная, увеличивается определитель, и уменьшаются ошибки параметров.

5. Переход от исходных объясняющих переменных к новым, представляющим линейные комбинации исходных. В качестве таких переменных используют, например, главные компоненты вектора исходных объясняющих переменных (Метод главных компонент).

Пример использования пошагового отбора факторов в модель.

Изучается зависимость индекса человеческого развития у от переменных:

Х₁ – ВВП 1997 г., % к 1992 г.;

Х₂ – расходы на конечное потребление в текущих ценах, % к ВВП;

Х₃ – расходы домашних хозяйств, % к ВВП;

Х₄ – валовое накопление, % к ВВП;

Х₅ – суточная калорийность питания населения, ккал на душу населениея;

Х₆ – ожидаемая продолжительность жизни при рождении в 1997 г., число лет.

Страна	Y	x1	x2	x3	x4	x5	x6	x1	x5	x2
Австрия		0,904		75,5	56,1	25,2					75,5
Австралия	0,922		78,5	61,8	21,8		78,2			78,5
Белоруссия	0,763		78,4	59,1	25,7					78,4
Бельгия		0,923		77,7	63,3	17,8		77,2			77,7
Великобритания	0,918		84,4	64,1	15,9		77,2			84,4
Германия		0,906		75,9		22,4		77,2			75,9
Дания		0,905			50,7	20,6		75,7
Индия		0,545		67,5	57,1	25,2		62,6			67,5
Испания		0,894		78,2		20,7					78,2
Италия		0,9		78,1	61,8	17,5		78,2			78,1
Канада		0,932		78,6	58,6	19,7					78,6
Казахстан	0,74			71,7	18,5		67,6
Китай		0,701		59,2		42,4		69,8			59,2
Латвия		0,744		90,2	63,9			68,4			90,2
Нидерланды	0,921		72,8	59,1	20,2		77,9			72,8
Норвегия		0,927		67,7	47,5	25,2		78,1			67,7
Польша		0,802		82,6	65,3	22,4		72,5			82,6
Россия		0,747		74,4	53,2	22,7		66,6			74,4
США		0,927		83,3	67,9	18,1		76,7			83,3
Украина		0,721		83,7	61,7	20,1		68,8			83,7
Финляндия	0,913		73,8	52,9	17,3		76,8			73,8
Франция		0,918		79,2	59,9	16,8		78,1			79,2
Чехия		0,833	99,2	71,5	51,5	29,9		73,9	99,2		71,5
Щвейцария	0,914		75,3	61,2	20,3		78,6			75,3
Швеция		0,923			53,1	14,1		78,5

1. Строим модель с полным перечнем факторов

ВЫВОД ИТОГОВ
Регрессионная статистика
Множественный R	0,98198162
R-квадрат	0,964287903
Нормированный R-квадрат	0,95238387
Стандартная ошибка	0,022104009
Наблюдения
Дисперсионный анализ
	df	SS	MS	F	Значимость F
Регрессия		0,237	0,040	81,00514774	4,86777E-12
Остаток		0,009	0,000
Итого		0,246
	Коэффициенты	Стандартная ошибка	t-статистика	P-Значение	Нижние 95%	Верхние 95%
Y-пересечение	-0,636	0,155	-4,109	0,001	-0,962	-0,311
x1	0,000	0,000	-2,088	0,051	-0,001	0,000
x2	0,001	0,001	0,895	0,383	-0,002	0,004
x3	-0,001	0,001	-1,141	0,269	-0,004	0,001
x4	0,000	0,001	0,107	0,916	-0,003	0,003
x5	0,000	0,000	2,114	0,049	0,000	0,000
x6	0,019	0,002	11,654	0,000	0,015	0,022

Уравнение статистически значимо, статистически не значимы коэффициенты b₁, b₂, b₃, b₄.

2. Рассчитаем корреляционную матрицу

	Y	x1	x2	x3	x4	x5	x6
Y
x1	-0,00434
x2	0,1705	-0,62897
x3	-0,00433	-0,36511	0,76495
x4	-0,48711	0,541074	-0,66713	-0,49626
x5	0,75145	0,077855	0,18551	0,109975	-0,33127
x6	0,96203	0,163276	0,04856	-0,05212	-0,40689	0,703927

3. Строим регрессию ух₆

ВЫВОД ИТОГОВ
Регрессионная статистика
Множественный R	0,962033161
R-квадрат	0,925507804
Нормированный R-квадрат	0,922269013
Стандартная ошибка	0,028241717
Наблюдения
Дисперсионный анализ
	df	SS	MS	F	Значимость F
Регрессия		0,227918365	0,227918365	285,757	1,8E-14
Остаток		0,018344675	0,000797595
Итого		0,24626304
	Коэффициенты	Стандартная ошибка	t-статистика	P-Значение	Нижние 95%	Верхние 95%
Y-пересечение	-0,652063486	0,089019418	-7,324957863	1,9E-07	-0,83621	-0,46791
x6	0,020178753	0,001193702	16,90435369	1,8E-14	0,01771	0,022648

4. Строим уравнения регрессии ух₆х₁, ух₆х₂, ух₆х₃. ух₆х₄. ух₆х₅

	ВЫВОД ИТОГОВ
	Регрессионная статистика
	Множественный R	0,975847
	R-квадрат	0,952277
	Нормированный R-квадрат	0,947938
	Стандартная ошибка	0,023113
	Наблюдения
	Дисперсионный анализ
		df	SS	MS	F	Значимость F
	Регрессия		0,234511	0,117255	219,4951	2,92E-15
	Остаток		0,011752	0,000534
	Итого		0,246263
		Коэффициенты	Стандартная ошибка	t-статистика	P-Значение	Нижние 95%	Верхние 95%
	Y-пересечение	-0,63377	0,073039	-8,67723	1,49E-08	-0,78525	-0,4823
	x6	0,020747	0,00099	20,95189	5,03E-16	0,018693	0,0228
	x1	-0,00055	0,000157	-3,51286	0,001963	-0,00088	-0,00023
	ВЫВОД ИТОГОВ
	Регрессионная статистика
	Множественный R	0,969983
	R-квадрат	0,940867
	Нормированный R-квадрат	0,935491
	Стандартная ошибка	0,025728
	Наблюдения
	Дисперсионный анализ
		df	SS	MS	F	Значимость F
	Регрессия		0,231701	0,11585	175,0217	3,09E-14
	Остаток		0,014562	0,000662
	Итого		0,246263
		Коэффициенты	Стандартная ошибка	t-статистика	P-Значение	Нижние 95%	Верхние 95%
	Y-пересечение	-0,79427	0,100574	-7,8973	7,31E-08	-1,00284	-0,58569
	x6	0,020052	0,001089	18,41813	7,4E-15	0,017794	0,02231
	x2	0,001968	0,000823	2,390465	0,02582	0,000261	0,003676

ВЫВОД ИТОГОВ
Регрессионная статистика
Множественный R	0,963126
R-квадрат	0,927613
Нормированный R-квадрат	0,921032
Стандартная ошибка	0,028466
Наблюдения
Дисперсионный анализ
	df	SS	MS	F	Значимость F
Регрессия		0,228437	0,114218	140,96	2,86E-13
Остаток		0,017826	0,00081
Итого		0,246263
	Коэффициенты	Стандартная ошибка	t-статистика	P-Значение	Нижние 95%	Верхние 95%
Y-пересечение	-0,70082	0,108474	-6,46068	1,69E-06	-0,92578	-0,47586
x6	0,020229	0,001205	16,79031	4,98E-14	0,01773	0,022728
x3	0,000766	0,000958	0,799796	0,432381	-0,00122	0,002754

ВЫВОД ИТОГОВ
Регрессионная статистика
Множественный R	0,967717
R-квадрат	0,936477
Нормированный R-квадрат	0,930702
Стандартная ошибка	0,026666
Наблюдения
Дисперсионный анализ
	df	SS	MS	F	Значимость F
Регрессия		0,23062	0,11531	162,1653	6,8E-14
Остаток		0,015643	0,000711
Итого		0,246263
	Коэффициенты	Стандартная ошибка	t-статистика	P-Значение	Нижние 95%	Верхние 95%
Y-пересечение	-0,53425	0,10353	-5,16033	3,58E-05	-0,74896	-0,31954
x6	0,0192	0,001234	15,56127	2,34E-13	0,016641	0,021759
x4	-0,00207	0,001062	-1,94908	0,064149	-0,00427	0,000132

ВЫВОД ИТОГОВ
Регрессионная статистика
Множественный R	0,967696
R-квадрат	0,936435
Нормированный R-квадрат	0,930657
Стандартная ошибка	0,026674
Наблюдения
Дисперсионный анализ
	df	SS	MS	F	Значимость F
Регрессия		0,230609	0,115305	162,0525	6,84E-14
Остаток		0,015654	0,000712
Итого		0,246263
	Коэффициенты	Стандартная ошибка	t-статистика	P-Значение	Нижние 95%	Верхние 95%
Y-пересечение	-0,63772	0,084402	-7,55566	1,5E-07	-0,81276	-0,46268
x5	4,64E-05	2,38E-05	1,944768	0,064696	-3,1E-06	9,58E-05
x6	0,018006	0,001587	11,34317	1,16E-10	0,014714	0,021298

Нормированный R2
Ryx6x1	0,9479
Ryx6x2	0,9355
Ryx6x3	0,9210
Ryx6x4	0,9307
Ryx6x5	0,9306

5. Строим уравнение регрессии ух₆х₁х₂, ух₆х₁х₃, ух₆х₁х₄, ух₆х₁х₅

ВЫВОД ИТОГОВ
Регрессионная статистика
Множественный R	0,976138
R-квадрат	0,952845
Нормированный R-квадрат	0,946108
Стандартная ошибка	0,023516
Наблюдения
Дисперсионный анализ
	df	SS	MS	F	Значимость F
Регрессия		0,23465	0,078217	141,4455	4,37E-14
Остаток		0,011613	0,000553
Итого		0,246263
	Коэффициенты	Стандартная ошибка	t-статистика	P-Значение	Нижние 95%	Верхние 95%
Y-пересечение	-0,67187	0,106108	-6,3319	2,81E-06	-0,89253	-0,4512
x6	0,020645	0,001028	20,0895	3,43E-15	0,018508	0,022782
x1	-0,00048	0,00021	-2,30955	0,031172	-0,00092	-4,8E-05
x2	0,000496	0,000986	0,502944	0,620238	-0,00156	0,002547

ВЫВОД ИТОГОВ
Регрессионная статистика
Множественный R	0,975952
R-квадрат	0,952481
Нормированный R-квадрат	0,945693
Стандартная ошибка	0,023606
Наблюдения
Дисперсионный анализ
	df	SS	MS	F	Значимость F
Регрессия		0,234561	0,078187	140,311	4,74E-14
Остаток		0,011702	0,000557
Итого		0,246263
	Коэффициенты	Стандартная ошибка	t-статистика	P-Значение	Нижние 95%	Верхние 95%
Y-пересечение	-0,61684	0,093455	-6,6004	1,55E-06	-0,81119	-0,42249
x6	0,020749	0,001011	20,51601	2,25E-15	0,018646	0,022852
x1	-0,00057	0,000172	-3,31518	0,003291	-0,00093	-0,00021
x3	-0,00026	0,000852	-0,30086	0,766478	-0,00203	0,001516
ВЫВОД ИТОГОВ
Регрессионная статистика
Множественный R	0,975876
R-квадрат	0,952333
Нормированный R-квадрат	0,945524
Стандартная ошибка	0,023643
Наблюдения
Дисперсионный анализ
	df	SS	MS	F	Значимость F
Регрессия		0,234524	0,078175	139,8529	4,89E-14
Остаток		0,011739	0,000559
Итого		0,246263
	Коэффициенты	Стандартная ошибка	t-статистика	P-Значение	Нижние 95%	Верхние 95%
Y-пересечение	-0,64446	0,100821	-6,39216	2,45E-06	-0,85413	-0,4348
x6	0,020866	0,001262	16,52766	1,63E-13	0,01824	0,023491
x1	-0,00058	0,000218	-2,64304	0,015208	-0,00103	-0,00012
x4	0,000201	0,001274	0,157911	0,876035	-0,00245	0,002852
ВЫВОД ИТОГОВ
Регрессионная статистика
Множественный R	0,980559
R-квадрат	0,961495
Нормированный R-квадрат	0,955994
Стандартная ошибка	0,021249
Наблюдения
Дисперсионный анализ
	df	SS	MS	F	Значимость F
Регрессия		0,236781	0,078927	174,7949	5,23E-15
Остаток		0,009482	0,000452
Итого		0,246263
	Коэффициенты	Стандартная ошибка	t-статистика	P-Значение	Нижние 95%	Верхние 95%
Y-пересечение	-0,62115	0,067386	-9,21774	7,91E-09	-0,76128	-0,48101
x6	0,01873	0,00128	14,63733	1,72E-12	0,016069	0,021391
x1	-0,00054	0,000145	-3,69691	0,001338	-0,00084	-0,00023
x5	4,26E-05	1,9E-05	2,242227	0,035871	3,09E-06	8,22E-05

Нормированный R2
Ryx6x1х2	0,9461
Ryx6x1х3	0,9457
Ryx6x1х4	0,9455
Ryx6x1х5	0,9560

6. Строим уравнение регрессии ух₆х₁х₅х₂, ух₆х₁х₅х₃, ух₆х₁х₅х₄

ВЫВОД ИТОГОВ
Регрессионная статистика
Множественный R	0,980559
R-квадрат	0,961497
Нормированный R-квадрат	0,953796
Стандартная ошибка	0,021774
Наблюдения
Дисперсионный анализ
	df	SS	MS	F	Значимость F
Регрессия		0,236781	0,059195	124,8592	7,6E-14
Остаток		0,009482	0,000474
Итого		0,246263
	Коэффициенты	Стандартная ошибка	t-статистика	P-Значение	Нижние 95%	Верхние 95%
Y-пересечение	-0,62333	0,100882	-6,17882	4,9E-06	-0,83376	-0,41289
x6	0,018731	0,001312	14,28188	5,93E-12	0,015995	0,021467
x1	-0,00053	0,000195	-2,71963	0,013198	-0,00094	-0,00012
x5	4,25E-05	2E-05	2,119958	0,046711	6,81E-07	8,43E-05
x2	2,79E-05	0,00094	0,029666	0,976628	-0,00193	0,001988
ВЫВОД ИТОГОВ
Регрессионная статистика
Множественный R	0,981161
R-квадрат	0,962676
Нормированный R-квадрат	0,955211
Стандартная ошибка	0,021438
Наблюдения
Дисперсионный анализ
	df	SS	MS	F	Значимость F
Регрессия		0,237072	0,059268	128,9629	5,58E-14
Остаток		0,009191	0,00046
Итого		0,246263
	Коэффициенты	Стандартная ошибка	t-статистика	P-Значение	Нижние 95%	Верхние 95%
Y-пересечение	-0,57869	0,086425	-6,69585	1,62E-06	-0,75897	-0,39841
x6	0,018588	0,001303	14,26201	6,08E-12	0,015869	0,021307
x1	-0,00058	0,000156	-3,70562	0,001399	-0,00091	-0,00025
x5	4,58E-05	1,96E-05	2,337282	0,029935	4,92E-06	8,66E-05
x3	-0,00063	0,00079	-0,79557	0,435621	-0,00228	0,00102
ВЫВОД ИТОГОВ
Регрессионная статистика
Множественный R	0,980631
R-квадрат	0,961636
Нормированный R-квадрат	0,953964
Стандартная ошибка	0,021734
Наблюдения
Дисперсионный анализ
	df	SS	MS	F	Значимость F
Регрессия		0,236816	0,059204	125,3321	7,33E-14
Остаток		0,009448	0,000472
Итого		0,246263
	Коэффициенты	Стандартная ошибка	t-статистика	P-Значение	Нижние 95%	Верхние 95%
Y-пересечение	-0,63799	0,092729	-6,88015	1,1E-06	-0,83142	-0,44456
x6	0,018907	0,001462	12,93174	3,59E-11	0,015857	0,021957
x1	-0,00057	0,0002	-2,85616	0,009762	-0,00099	-0,00015
x5	4,29E-05	1,95E-05	2,202278	0,039545	2,26E-06	8,35E-05
x4	0,000318	0,001173	0,271507	0,788784	-0,00213	0,002765

Нормированный R2
Ryx6x1х5х2	0,9537
Ryx6x1х5х3	0,9552
Ryx6x1х5х4	0,9540

При добавлении 4-го фактора коэффициент детерминации не увеличивается. Поэтому 4-й фактор лишний, и наилучшей является регрессия ух₆х₁х₅:

,

Уравнение значимо, все коэффициенты значимы, R² = 0,956.