Мультиграфы. Эйлеров цикл. Эйлеров граф

В 1736г. Леонард Эйлер решил задачу о кёнигсбергских мостах. Четыре части суши – два берега (точки A и D) и два острова (точки B и C) соединены семью мостами: надо прогуляться по замкнутому маршруту, так, чтобы пройти через каждый из мостов только один раз.

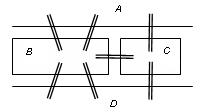
Решение задачи сводится к рассмотрению мультиграфа и к поиску в нем замкнутого маршрута, проходящего через все ребра ровно по одному разу:

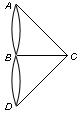
Эйлеров цикл в мультиграфе – это цикл, содержащий все ребра.

Граф называется эйлеровым, если содержит эйлеров цикл.

Пример эйлерова графа:

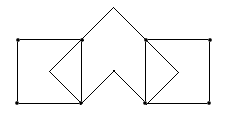
Граф называется связным, если любые его две вершины соединены некоторой цепью.

Теорема. Граф G эйлеров тогда и только тогда, когда граф G связный граф и степень каждой вершины графа G есть чётное число.

Доказательство. Если граф G эйлеров, т.е. содержит цикл, проходящий через все ребра графа G, то, значит, граф связный, а каждая вершина графа инцидентна четному числу ребер: вместе с каждым ребром – «входом» цикла в вершину должно быть ребро – «выход» цикла из вершины.

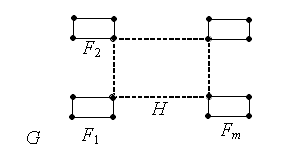
Обратно, индукцией по числу ребер доказываем, что если граф G связный, а каждая вершина графа инцидентна четному числу ребер, то в графе найдется подграф – эйлеров цикл. Поскольку граф связный и степени вершин – четные числа, то степень каждой вершины не меньше 2, значит, в графе G найдется хотя бы один цикл H. Разность G \ H распадается на связные компоненты, содержащие тоже вершины с четными степенями, значит, по индуктивному предположению, содержащие эйлеровы циклы F ₁, …, F_m. Соединяя подходящим образом граф H с графами F ₁, …, F_m, получим эйлеров цикл в графе G.