Теорема об эйлеровых графах

Связный граф будет эйлеровым тогда и только тогда, когда степень каждой вершины четная.

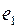Доказательство. Пусть граф эйлеров, т.е. существует цикл, проходящий по всем ребрам графа по одному разу. Если в вершину пришли по ребру , то должно существовать ребро 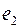, по которому из этой вершины можно выйти. Если в эту же вершину попали еще раз, то уже по ребру 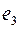и выходим по ребру 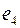. Число ребер, по которым мы попадаем в некоторую вершину равно числу ребер, по которым мы из нее выходим, следовательно, 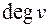– четное число.

Пусть 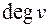– четное число для любой вершины и граф связен. Покажем, что в этом случае существует цикл, проходящий по всем ребрам по одному разу. Возьмем вершину 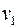и пойдем из нее по ребрам и вершинам графа так далеко, насколько это возможно. Ребра в этом пути не должны повторяться. Если мы пришли в вершину по некоторому ребру, то выйдем из нее по другому ребру, это возможно, так как 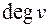– четное число. Этот путь завершится в вершине 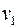, так как только у нее осталось нечетное число неиспользованных ребер. Таким образом, мы получили цикл 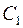, если в него вошли все ребра графа, то теорема доказана. Если остались ребра графа, не вошедшие в цикл 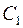, то благодаря связности графа хотя бы одно из них должно быть инцидентно какой-либо вершине, вошедшей в 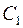, назовем ее 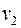. Из вершины 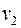пойдем по неиспользованным ребрам, этот путь завершится в вершине 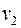, получим цикл 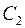. Рассмотрим цикл 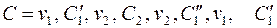и 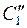– последовательности вершин и ребер цикла 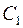. Если в цикл 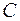вошли все ребра графа , то 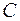– эйлеров цикл, если нет, то повторим процедуру.

Определение. Граф называется полуэйлеровым, если в нем существует цепь, проходящая по всем ребрам по одному разу.

Теорема. Связный граф будет полуэйлеровым тогда и только тогда, когда в нем существуют ровно 2 вершины нечетной степени.

Теорема Дирака (достаточное условие гамильтоновости неориентированного графа).

Если 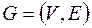связный простой граф с 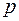вершинами и для любой вершины 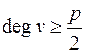, то в нем существует гамильтонов цикл.

Доказательство. Пусть условия теоремы выполняются и, тем не менее, не является гамильтоновым графом, т.е. существует вершина из которой нельзя попасть в вершину 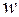. Тогда добавим к графу новых вершин, соединим их со всеми вершинами графа так, чтобы полученный граф 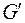стал гамильтоновым, и пусть – минимальное число требуемых вершин.

В 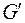существует гамильтонов цикл: 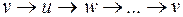, где 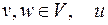– вновь добавленная вершина.

Удалить ее нельзя, так как вершины и 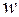не являются смежными по предположению. С другой стороны, не может быть цикла вида 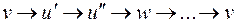, где добавленные вершины 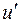и 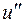смежны, так как мы добавляем минимальное число новых вершин.

Не может быть и такого случая: 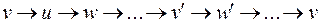, где 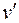смежна с , а 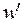смежна с 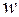. В этом случае можно было бы перевернуть часть цикла от 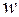до 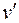: 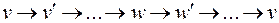и обойтись без добавления вершины 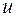для получения гамильтонова цикла.

Число вершин в графе 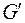, смежных с вершиной (или 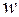) не меньше, чем 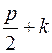, так как степень вершины не меньше чем 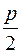, а добавленные вершины смежны со всеми вершинами графа по построению.

Рассмотрим вершины, не смежные с 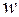. Так как вершина 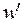, смежная с 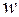, не может идти в цикле сразу за вершиной 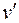, смежной с , то вершин, не смежных с 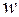должно быть не меньше, чем вершин, смежных с (в цепочке должно быть 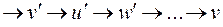), то есть не меньше, чем 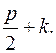Тогда общее число вершин в графе 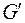не меньше, чем 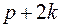. С другой стороны их ровно 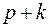, отсюда 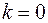и теорема доказана.