Циклы
Задачи
4.1. Используя метод поиска в ширину, найдите компоненты связности графа, заданного
матрицей смежности:

4.2. Методом поиска в ширину постройте дерево кратчайших путей из вершины 1 для
графа, заданного списками смежности:
1: 2,9; 3: 2, 7; 5: 4, 6, 7, 9, 10; 7: 2, 3, 5, 6, 8; 9: 1, 4. 5, 8, 10;
2: 1, 3, 7, 8; 4: 5, 9; 6: 5, 7, 10; 8: 2, 7, 9; 10: 5, 6, 9
4.3. Лес задан списками смежности. Какие из следующих оценок времени работы верны
для поиска в ширину?
1) 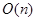 ; 2)
; 2) 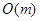 ; 3)
; 3) 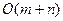 ; 4)
; 4) 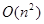 ; 5)
; 5) 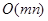 .
.
4.4. Лес задан матрицей смежности. Какие из следующих оценок времени работы верны
для поиска в ширину?
1) 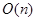 ; 2)
; 2) 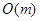 ; 3)
; 3) 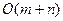 ; 4)
; 4) 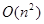 ; 5)
; 5) 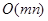 .
.
4.5. Какова будет высота BFS-дерева, если поиск в ширину применяется к графу
1) 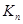 ; 2)
; 2) 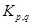 ,
, 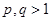 ; 3)
; 3) 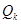 ; 4)
; 4) 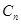 ; 5)
; 5) 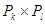 , старт в вершине степени 2?
, старт в вершине степени 2?
4.6. Пусть h –высота BFS-дерева для графа G. Может быть 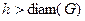 ?
? 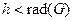 ?
?
Всегда ли можно выбрать стартовую вершину так, чтобы было 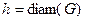 ?
?
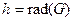 ?
?
4.7. Ребро 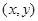 является обратным ребром относительно BFS-дерева с корнем
является обратным ребром относительно BFS-дерева с корнем 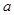 . Какие
. Какие
из следующих соотношений могут выполняться? А если граф двудольный?
1) 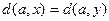 ; 3)
; 3) 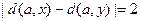 ;
;
2) 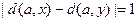 ; 4)
; 4) 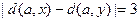 .
.
4.8. Два человека имеют восьмилитровый кувшин, наполненный вином, и два пустых
кувшина:
а) трехлитровый и двухлитровый;
б) пятилитровый и шестилитровый.
Они могут переливать вино из одного кувшина в другой, пока либо первый не
опустеет, либо второй не наполнится. Могут они разделить вино поровну с помощью
таких действий? Какое наименьшее число переливаний потребуется?
4.9. Используя алгоритм поиска в глубину, найдите компоненты связности графа,
заданного списками смежности:
1: 2, 4, 6; 3: 5, 9; 5: 3, 9; 7: 8, 10; 9: 3, 5; 11: 8, 12;
2: 1; 4: 1; 6: 1; 8: 7, 10, 11; 10: 7, 8, 12; 12: 10, 11.
4.10. Постройте DFS-дерево с корнем в вершине 1 для графа, заданного списками
смежности:
1: 5, 6, 7, 8; 3: 2, 4; 5: 1, 6, 10; 7: 1, 2, 4, 8; 9: 8;
2: 3, 4, 7, 8; 4: 2, 3, 7: 6: 1, 5; 8: 1, 2, 7, 9; 10: 5.
4.11. Планарный граф задан списками смежности. Какие из следующих оценок времени
работы верны для поиска в глубину?
1) 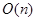 ; 2)
; 2) 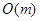 ; 3)
; 3) 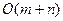 ; 4)
; 4) 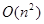 ; 5)
; 5) 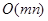 .
.
4.12. Планарный граф задан матрицей смежности. Какие из следующих оценок времени
работы верны для поиска в глубину?
1) 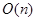 ; 2)
; 2) 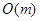 ; 3)
; 3) 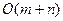 ; 4)
; 4) 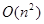 ; 5)
; 5) 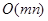 .
.
4.13. Дерево задано списками смежности. Какие из следующих оценок времени работы
верны для поиска в глубину?
1) 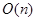 ; 2)
; 2) 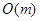 ; 3)
; 3) 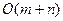 ; 4)
; 4) 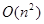 ; 5)
; 5) 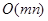 .
.
4.14. Сколько различных DFS-деревьев можно построить для графа 1)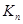 ; 2)
; 2)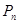 ; 3)
; 3)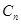 ?
?
4.15. Пусть h –высота DFS-дерева для графа G. Может быть a)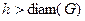 ?
?
б)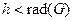 ?
?
4.16. Какой может быть максимальная высота DFS-дерева, если поиск в глубину
применяется к графу 1) 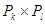 ; 2)
; 2) 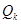 ; 3)
; 3) 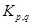 ,
, 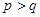 ?
?
4.17. Ребро 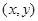 является обратным ребром относительно DFS-дерева с корнем
является обратным ребром относительно DFS-дерева с корнем 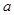 .
.
Какие из следующих соотношений могут выполняться ( обозначает расстояние
обозначает расстояние
между вершинами в графе)? А если граф двудольный?
1) 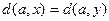 ; 3)
; 3) 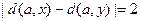 ;
;
2) 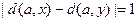 ; 4)
; 4) 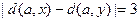 .
.
4.18. Построить DFS-дерево и таблицы функций 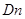 и
и 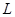 для графа, заданного списками
для графа, заданного списками
смежности:
1: 3, 4 3: 1, 6 5: 2, 7, 11 7: 5, 6, 10 9: 6, 8 11: 5,7,12
2: 5 4: 1, 6 6: 3, 4, 8, 9 8: 6, 9 10: 7 12: 11.
Найти все шарниры и блоки этого графа, построить BC-дерево.
4.19. Каждый блок графа состоит из трех вершин. Сколько вершин и ребер в этом графе,
если его BC-дерево представляет собой а) путь 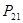 ; б) путь
; б) путь 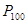 ; в) граф
; в) граф 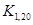 ?
?
4.20*. Разработайте алгоритм, который за время 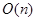 проверяет, является ли данный граф
проверяет, является ли данный граф
деревом.
4.21*. Разработайте алгоритм, проверяющий, является ли данный граф двудольным.
4.22*. Разработайте алгоритм, который находит кратчайший цикл, проходящий через
данную вершину.
4.23*. Докажите, что описанный выше алгоритм нахождения центра дерева с помощью
двойного обхода в ширину действительно находит центр любого дерева.
Приведите пример графа, для которого это не так.
4.24*. Доработайте алгоритм выявления шарниров так, чтобы он правильно обрабатывал
корень DFS-дерева (т.е. решал, является ли эта вершина шарниром).
4.25*. Разработайте алгоритм, определяющий, является ли данное ребро перешейком
графа.
4.26*. Разработайте алгоритм выявления всех перешейков графа.
4.27*. (Задача об одностороннем движении) Докажите, что ребра обыкновенного графа
можно ориентировать так, что получится сильно связный орграф, тогда и только
тогда, когда в нем нет перешейков. Разработайте алгоритм построения такой
ориентации.
Эйлеровы циклы
Эйлеровым циклом (путем) называется цикл (путь), проходящий через все ребра графа. Граф, в котором имеется эйлеров цикл, называют эйлеровым графом.
Теорема об эйлеровом цикле. Связный граф эйлеров тогда и только тогда, когда в нем степени всех вершин четны.
Следствие (об эйлеровом пути). Эйлеров путь в связном графе существует тогда и только тогда, когда в нем имеется не более двух вершин нечетной степени.
Ниже приводится алгоритм построения эйлерова цикла. Предполагается, что условия существования уже проверены – граф связен и степени четны. В алгоритме строится путь, начинающийся в произвольно выбранной стартовой вершине a, при этом каждый раз для дальнейшего продвижения выбирается любое еще не пройденное ребро. Вершины пути накапливаются в стеке S (они могут повторяться). Когда наступает тупик – все ребра, инцидентные последней вершине пути, уже пройдены, производится возвращение вдоль пройденного пути, пока не встретится вершина, которой инцидентно не пройденное ребро. При возвращении вершины перекладываются из стека S в другой стек C. Затем возобновляется движение вперед по не пройденным ребрам, пока снова не наступает тупик, и т. д. Процесс заканчивается, когда стек S оказывается пустым. В этот момент в стеке C находится последовательность вершин эйлерова цикла.
1 выбрать произвольно вершину а;
2 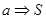 ;
;
3 while 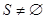 do
do
4 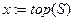 ;
;
5 if имеется не пройденное ребро 
6 then пометить ребро  как пройденное;
как пройденное;
7  ;
;
8 else переместить вершину x из S в C
Трудоемкость этого алгоритма оценивается как 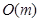 . Этот вывод справедлив лишь при определенных предположениях о том, как задан граф. Можно, например, использовать две структуры:
. Этот вывод справедлив лишь при определенных предположениях о том, как задан граф. Можно, например, использовать две структуры:
- массив ребер, в котором в позиции, соответствующей ребру, помещается запись, указывающая две вершины этого ребра и пометку о том, пройдено ли это ребро;
- списки инцидентности, в которых для каждой вершины перечисляются инцидентные ей ребра.
В ориентированном графе эйлеров цикл – это ориентированный цикл, проходящий через все ребра.
Теорема об эйлеровом цикле в орграфе. Эйлеров цикл в сильно связном орграфе существует тогда и только тогда, когда в нем для каждой вершины х выполняется равенство 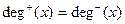 .
.
Одно из применений эйлеровых циклов в орграфе – построение так называемых последовательностей де Брейна. Слово 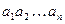 в алфавите {0,1} является последовательностью де Брейна порядка k, если в слове
в алфавите {0,1} является последовательностью де Брейна порядка k, если в слове 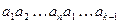 среди отрезков длины k каждое слово длины k встречается ровно один раз. Иначе говоря, если последовательность де Брейна свернуть в кольцо и двигать вдоль этого кольца окно, в котором видны k последовательных букв, то в течение одного оборота каждое слово длины k появится в окне один раз. Ясно, что
среди отрезков длины k каждое слово длины k встречается ровно один раз. Иначе говоря, если последовательность де Брейна свернуть в кольцо и двигать вдоль этого кольца окно, в котором видны k последовательных букв, то в течение одного оборота каждое слово длины k появится в окне один раз. Ясно, что 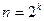 . Пример последовательности де Брейна порядка 3: 00010111.
. Пример последовательности де Брейна порядка 3: 00010111.
Для построения последовательностей де Брейна можно использовать граф де Брейна. Вершинами этого графа являются всевозможные слова длины 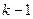 , из каждой вершины
, из каждой вершины 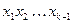 выходят ровно два ребра: в вершины
выходят ровно два ребра: в вершины 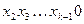 и
и 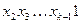 . Первому ребру приписывается буква 0, второму – буква 1. Очевидно, входящих ребер тоже будет два: из вершин
. Первому ребру приписывается буква 0, второму – буква 1. Очевидно, входящих ребер тоже будет два: из вершин 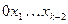 и
и 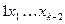 . Очевидно также, что этот граф сильно связен – от любого слова можно перейти к любому другому, добавляя буквы в конце. Значит, в нем имеется эйлеров цикл. Двигаясь вдоль такого цикла и выписывая буквы, приписанные ребрам, получим последовательность де Брейна. На рисунке 6 показан граф де Брейна для
. Очевидно также, что этот граф сильно связен – от любого слова можно перейти к любому другому, добавляя буквы в конце. Значит, в нем имеется эйлеров цикл. Двигаясь вдоль такого цикла и выписывая буквы, приписанные ребрам, получим последовательность де Брейна. На рисунке 6 показан граф де Брейна для 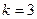 .
.
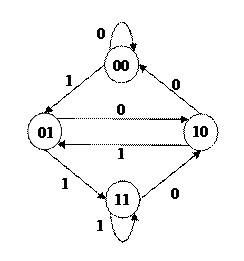
Рис. 6.
Гамильтоновы циклы
Гамильтоновым циклом (путем) называют простой цикл (путь), содержащий все вершины графа.
Внешне определение гамильтонова цикла похоже на определение эйлерова цикла. Однако есть кардинальное различие в сложности решения соответствующих задач. Мы видели, что имеется достаточно простой критерий существования эйлерова цикла и эффективный алгоритм его построения. Для гамильтоновых же циклов (и путей) неизвестно никаких просто проверяемых необходимых и достаточных условий их существования, а все известные алгоритмы требуют для некоторых графов перебора большого числа вариантов. Такие задачи называют задачами переборного типа или неподдающимися задачами. Очень многие известные задачи относятся к разряду неподдающихся, среди них немало задач на графах. Существует математическая теория сложности алгоритмов и задач, в которой под эффективным алгоритмом понимают алгоритм, время работы которого ограничено сверху полиномом от длины записи входных данных. Выводы этой теории делают весьма правдоподобным предположение о том, что для многих неподдающихся задач, в том числе и для задачи о гамильтоновом цикле, не существует эффективных алгоритмов.
Перебор вариантов в задаче о гамильтоновом цикле (построить гамильтонов цикл или убедиться, что его не существует) можно организовать с помощью дерева путей. Это дерево представляет всевозможные простые пути в данном графе, начинающиеся в некоторой вершине а. Его вершины соответствуют вершинам графа, при этом каждая вершина графа может быть представлена в дереве несколько раз. Оно может быть построено следующим образом. Выберем в графе произвольно вершину а и объявим ее корнем дерева. Вершины, смежные с а, добавим к дереву в качестве сыновей вершины а. Для каждой вершины b, добавленной к дереву, рассмотрим все смежные с ней вершины и те из них, которые не лежат на пути (в дереве) из a в b, добавим к дереву в качестве сыновей вершины b. Процесс построения дерева заканчивается, когда к нему уже невозможно добавить новую вершину. Очевидно, что каждому пути в дереве, начинающемся в корне, соответствует точно такой же (простой) путь в графе, и обратно, каждому простому пути в графе с началом в вершине а соответствует такой же путь в дереве. Каждой вершине, находящейся в дереве на расстоянии 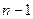 от корня, соответствует гамильтонов путь в графе с началом в вершине а, а если последняя вершина этого пути смежна с а, то получаем гамильтонов цикл. Если высота дерева путей не превосходит
от корня, соответствует гамильтонов путь в графе с началом в вершине а, а если последняя вершина этого пути смежна с а, то получаем гамильтонов цикл. Если высота дерева путей не превосходит 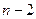 , то в графе нет гамильтоновых путей, начинающихся в а, и нет гамильтоновых циклов. На рисунке 7 показаны граф и его дерево путей из вершины 1.
, то в графе нет гамильтоновых путей, начинающихся в а, и нет гамильтоновых циклов. На рисунке 7 показаны граф и его дерево путей из вершины 1.
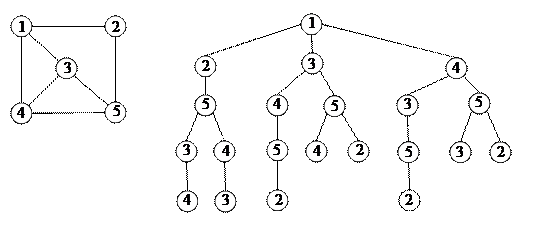
Рис. 7.
Дерево путей можно построить с помощью процедуры типа поиска в ширину: вершины исследуются и добавляются к дереву в порядке возрастания их расстояний (в дереве) от корня. Отличие от обычного поиска в ширину состоит в том, что вершина графа может добавляться к дереву несколько раз.
Дерево путей может быть очень большим. Для полного графа 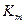 в этом дереве будет
в этом дереве будет 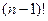 листьев. Однако, если задача состоит в том, чтобы найти один гамильтонов путь или цикл (если такой существует), то совсем не обязательно строить это дерево целиком. Можно организовать обход этого дерева с помощью, скажем, поиска в глубину, без его явного построения. Для полного графа такой алгоритм даст ответ очень быстро, но в некоторых случаях время его работы тоже растет с факториальной скоростью. Например, для графа
листьев. Однако, если задача состоит в том, чтобы найти один гамильтонов путь или цикл (если такой существует), то совсем не обязательно строить это дерево целиком. Можно организовать обход этого дерева с помощью, скажем, поиска в глубину, без его явного построения. Для полного графа такой алгоритм даст ответ очень быстро, но в некоторых случаях время его работы тоже растет с факториальной скоростью. Например, для графа 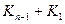 , если в качестве стартовой выбрана не изолированная вершина, будут рассмотрены все
, если в качестве стартовой выбрана не изолированная вершина, будут рассмотрены все 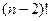 простых путей длины
простых путей длины 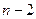 в большой компоненте.
в большой компоненте.
Кодом Грея порядка 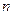 называется расположение всех
называется расположение всех 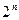 двоичных слов длины
двоичных слов длины 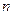 в последовательность, в которой любые два соседних слова различаются ровно в одной букве. Двоичные слова длины n можно рассматривать как вершины графа
в последовательность, в которой любые два соседних слова различаются ровно в одной букве. Двоичные слова длины n можно рассматривать как вершины графа  – ребра этого графа соединяют как раз пары слов, различающихся в одной букве. Значит, код Грея есть не что иное, как гамильтонов путь в графе
– ребра этого графа соединяют как раз пары слов, различающихся в одной букве. Значит, код Грея есть не что иное, как гамильтонов путь в графе  . Существование такого пути при любом n легко доказать с помощью индукции, используя равенство
. Существование такого пути при любом n легко доказать с помощью индукции, используя равенство 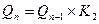 .
.
В ориентированном графе гамильтонов цикл (путь) – это ориентированный цикл (путь), проходящий через каждую вершину точно один раз. Задачи о гамильтоновых циклах и путях для орграфов в общем случае тоже неподдающиеся. В то же время имеется важный класс графов, для которых эти задачи имеют простое решение. Это так называемые турниры.
Орграф называется турниром, если для каждых двух вершин в нем имеется единственное ребро, соединяющее эти вершины.
Теорема о гамильтоновых путях в турнирах. В любом турнире имеется гамильтонов путь.
Для нахождения гамильтонова пути в турнире можно использовать следующее легко доказываемое свойство: если 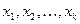 – ориентированный простой путь в турнире, y – вершина, не принадлежащая этому пути, то хотя бы одна из последовательностей
– ориентированный простой путь в турнире, y – вершина, не принадлежащая этому пути, то хотя бы одна из последовательностей 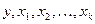 ,
, 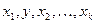 , …,
, …, 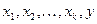 тоже является ориентированным простым путем.
тоже является ориентированным простым путем.
Аналогично обстоит дело с гамильтоновыми циклами в турнирах (см. задачу 5.25).
 2014-02-04
2014-02-04 4100
4100








