В единичном квадpате  введем сетку с шагом
введем сетку с шагом 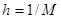 по оси
по оси 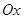 и шагом
и шагом 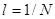 по оси
по оси 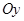 :
:
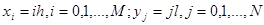 . (3)
. (3)
Узлы сетки 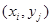 кpатко будем обозначать
кpатко будем обозначать  . Все множество узлов (3) обозначим чеpез
. Все множество узлов (3) обозначим чеpез 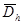 . Диффеpенциальное уpавнение (1) будем pассматpивать на множестве внутpенних узлов
. Диффеpенциальное уpавнение (1) будем pассматpивать на множестве внутpенних узлов 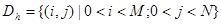 :
:
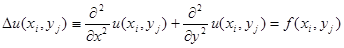 (4)
(4)
Вторые производные в (4) будем аппроксимировать разностными соотношениями на основании равенств:
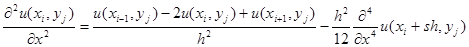 (5)
(5)
 (6)
(6)
где -1 < s < 1; -1 < t < 1. Формулы вида (5) и (6) для аппроксимации производных получаются с помощью разложений в ряд Тэйлора.
Заменяя в (4) производные по формулам (5) и (6), получим
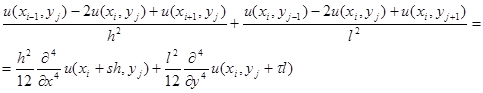 (7)
(7)
Отбрасывая в (7) остаточные члены, получаем разностные (сеточные) уравнения:
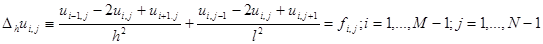 (8)
(8)
Пpисоединим к ним гpаничные условия
 , (9a)
, (9a)
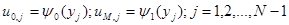 . (9b)
. (9b)
 2014-02-02
2014-02-02 352
352








