2014-02-02
1388
Общий вид дифференциальной краевой задачи. Общий вид соответствующей разностной схемы. Определения сходимости, аппроксимации, устойчивости. Теорема о связи аппроксимации и устойчивости со сходимостью.
Последовательное использование определений устойчивости, аппроксимации и сходимости при доказательстве теоремы.
Пусть в области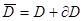 
задана краевая задача
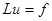, (1)
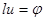. (2)
Обозначим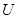 
- пространство функций, определенных на замкнутом множестве 
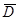, к которому мы относим решение задачи (1), (2); 
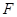- пространство правых частей 
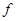, определенных на 
, и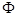 
- пространство функций, определенных на границе 
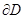области.
На множестве 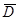введем сетку 
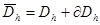и построим разностную схему
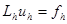, (3)
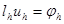. (4)
Обозначим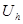 
- пространство функций, определенных на всей сетке 
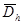, к которому мы относим решение задачи (3), (4); 
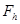- пространство правых частей 
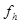, определенных на 
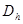, и 
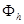- пространство функций 
, определенных на границе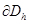 
сетки.
Проекцию непрерывной функции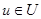 
обозначим через 
.
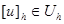В пространствах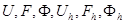 
введем нормы. При этом сеточные нормы в пределе при 
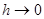должны совпадать с непрерывными нормами.
Определение 1. Говорят, что решение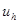 
разностной схемы (3), (4) сходится к решению 
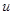краевой задачи (13), (14), если
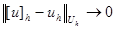при .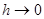
Определение 2. Говорят, что разностная схема (3), (4) аппроксимирует краевую задачу (1), (2) на ее решении 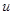, если
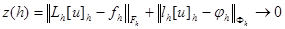при .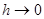
При этом величину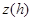
называют погрешностью аппроксимации на решении.
Определение 3. Разностную схему (3), (4) называют устойчивой, если существуют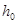 
и не зависящие от 
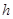константы 
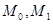, такие, что при 
для любой сеточной функции 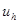выполняется неравенство
.
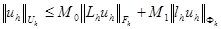Теорема. Если разностная схема (3), (4) устойчива и аппроксимирует краевую задачу (1), (2) на ее решении, то решение 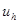разностной схемы сходится к решению 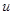краевой задачи.
Доказательство. Для сеточной функции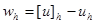 
, в силу устойчивости разностной схемы, имеем 
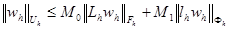или 
. Учитывая линейность операторов, разностную схему и условие аппроксимации, отсюда получаем
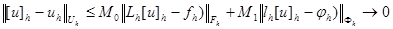при .
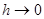Доказанная теорема позволяет разбить исследование сходимости на два этапа: исследование аппроксимации и исследование устойчивости разностной схемы.
При изложении материала за основу взяты
1) страницы 481-490 учебного пособия: Бахвалов Н.С., Жидков Н.П., Кобельков Г.М.. Численные методы: Учеб. пособие для вузов.- М.:Наука. Гл. ред. физ.-мат. лит., 1987.
2) страницы 135-151 учебного пособия:Крылов В.И., Бобков В.В., Монастырный П.И. Вычислительные методы:, т.2.-М.:Наука. Гл. ред. физ.-мат. лит., 1977.
3) страницы 286-291 учебного пособия: Самарский А.А., Гулин А.В. Численные методы.- М.: Наука, 1989.
11.3. Сходимость сеточного метода
решения краевой задачи для уравнения Пуассона.
Задача Дирихле для уравнения Пуассона в единичном квадрате и ее разностная схема. Определения аппроксимации, устойчивости, сходимости и связь между ними.
Использование введенных сеточных норм, вспомогательного квадратного многочлена и принципа максимума для исследования устойчивости разностной схемы.
