Закон компандирования µ
Этот закон отличается большим числом дискрет для кодирования сигнала. Их — 8159, что позволяет более точно кодировать слабые сигналы. По статистике их больше, чем сигналов с большой амплитудой. Это обстоятельство повышает качество речи (но, как показала практика, незначительно). При этом шаги квантования меняются в каждом сегменте и равны 1, 2, 4, 8, 16, 32, 64, 128, 256. Ниже приводится таблица кодирования (табл. 1.6).
Таблица 1.6. Кодирование сегментов согласно закону µ
| Диапазон входных амплитуд | Размер шага | Код сегмента* | Код шага квантования | Амплитуда на выходе декодера |
| 0-1 | ||||
| 1-3 | ||||
| 3-5 | ||||
| 29-31 | ||||
| 31-35 | ||||
| 91-95 | ||||
| 95-103 | ||||
| 215-223 | ||||
| 223-239 | ||||
| 463-479 | ||||
| 479-511 | ||||
| 959-991 | ||||
| 991-1055 | ||||
| 1951-2015 | ||||
| 2015-2143 | ||||
| 3935-4063 | ||||
| 4063-4319 | ||||
| 7903-8159 | ||||
| * Все значения кодовых комбинаций инвертируются. |
Получение кода для передачи в линию в данном случае немного сложнее, чем при использовании А-закона. Кодированию подлежат значения отсчетов, увеличенные на 33. На приемном конце после декодирования полученное значение надо уменьшить на эту величину.
Номер сегмента здесь определяется по положению «ведущей» единицы (при законе А этой единицы в первом сегменте нет) и так же, как в предыдущем случае, равно разности между числом нулей до первой единицы слева и цифрой 7 (объяснение этого факта аналогично объяснению для А-закона и следует из принципов двоичной нумерации).
Значение кода шага квантования определяется, как и в предыдущем случае, отбрасыванием младших разрядов в соответствии с точностью квантования, принятой на данном шаге.
Декодирование производится путем подстановки на место отброшенных разрядов комбинации из единицы в старшем разряде и остальных нулей. Процессы кодирования и декодирования показаны в табл. 1.7 и 1.8. Число разрядов в получаемой линейной комбинации равно 13 (для отображения максимального значения, равного 8159).
Таблица 1.7. Линейные комбинации, передаваемые в канал согласно закону µ
| Кодовая линейная комбинация | Комбинация, передаваемая в канал |
| 0000001 wxyz- | 000 wxyz |
| 00000 lwxyz-- | 001wxyz |
| 0000 lwxyz-- | 010wxyz |
| 0000 lwxyz | 011 wxyz |
| OOOlwxyz | 100wxyz |
| OOlwxyz | 101 wxyz |
| Olwxyz | 110wxyz |
| lwxyz | 111 wxyz |
Таблица 1.8. Восстановление компрессированных комбинаций на приемном конце согласно закону µ
| Кодовые комбинации, полученные при компрессировании | Кодовые комбинации линейного выхода |
| 000 wxyz | 00000001 wxyzl |
| 001 wxyz | 000000 lwxyz 10 |
| 010wxyz | 00000 lwxyz 100 |
| 011 wxyz | 0000 lwxyz 1000 |
| 100 wxyz | 000 lwxyz 10000 |
| 101 wxyz | 001 wxyzl 00000 |
| 110 wxyz | 01 wxyzl 000000 |
| 111 wxyz | lwxyz10000000 |
Сигналы, полученные методом ИКМ, позволяют мультиплексировать информацию по времени. Для этого периодически подаваемые сигналы одного канала надо сдвинуть по времени относительно сигналов другого канала так, чтобы они поступали во время паузы в первом, как это показано на рис. 24. На нем показаны четыре канала, по каждому из которых периодически поступает информация. При объединении в один тракт эти сигналы поступают в определенные промежутки времени.
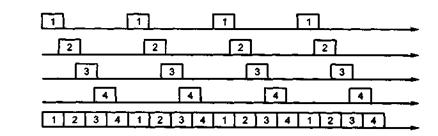
Рис. 24. Принцип мультиплексирования
В наиболее распространенной для Европы системе ИКМ, которая легла в основу всех цифровых систем коммутации, количество каналов в одном цифровом тракте равно 32.
Если вспомнить, что для каждого цифрового канала надо передавать 64 килобита в одну секунду, то для передачи 32 каналов требуется передавать 2048 килобит в секунду.
 2014-02-02
2014-02-02 628
628








