Пусть функция 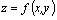 определена в области G и точка
определена в области G и точка 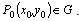 . Дадим абсциссе
. Дадим абсциссе 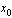 приращение
приращение 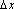 , тогда функция z получит приращение
, тогда функция z получит приращение 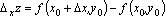 , которое называется частным приращением по x функции
, которое называется частным приращением по x функции 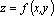 в точке
в точке 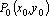 .
.
Частной производной по x функции в точке называется предел отношения частного приращения по x функции в точке к приращению при стремлении к нулю.
Обозначают частную производную функции z по переменной x 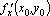 ,
,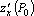 ,
, 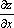 .
.
Таким образом, 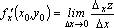
Аналогично определяются частное приращение по y функции 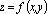 в точке
в точке 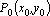 :
: 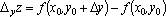 и частная производная по y функции
и частная производная по y функции 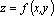 в точке
в точке 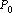 :
:
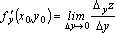 (обозначают также
(обозначают также 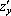 ,
, 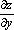 ).
).
Заметив, что вычисляется при неизменном y, а 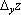 – при неизменном x, можно сделать вывод: правила вычисления частных производных совпадают с правилами дифференцирования функций одной переменной, но при вычислении
– при неизменном x, можно сделать вывод: правила вычисления частных производных совпадают с правилами дифференцирования функций одной переменной, но при вычислении  полагают
полагают 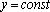 , а при вычислении
, а при вычислении 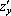 полагают
полагают 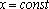 .
.
Примеры:
1) 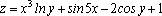 ;
;
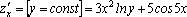 ;
;
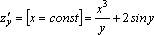 .
.
2) 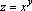 ;
; 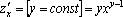 ;
; 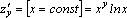 .
.
Для функции 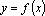 одной переменной производная n–го порядка определялась следующим образом:
одной переменной производная n–го порядка определялась следующим образом: 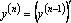 . Аналогично определяются и частные производные высших порядков.
. Аналогично определяются и частные производные высших порядков.
Частной производной n–го порядка функции нескольких переменных называется частная производная первого порядка от частной производной (n–1)–го порядка той же функции.
|
|
|
При этом учитывается, что производные можно вычислять по различным переменным. Так, функция двух переменных 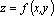 имеет две частных производных 1–го порядка:
имеет две частных производных 1–го порядка: 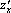 и
и 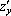 , четыре частных производных 2–го порядка:
, четыре частных производных 2–го порядка:
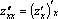 ,
, 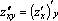 ,
, 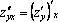 ,
, 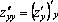 , восемь частных производных 3–го порядка (от каждой из четырех производных 2–го порядка можно найти производную как по x, так и по y), например,
, восемь частных производных 3–го порядка (от каждой из четырех производных 2–го порядка можно найти производную как по x, так и по y), например, 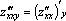 ,
, 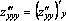 .
.
Частные производные высших порядков обозначают также 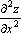 ,
, 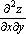 ,
,  ,
, 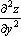 ,
, 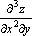 ,
, 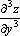 . Частная производная 2–го или более высокого порядка, взятая по нескольким различным переменным, называется смешенной частной производной.
. Частная производная 2–го или более высокого порядка, взятая по нескольким различным переменным, называется смешенной частной производной.
Справедлива теорема:
Две смешанные частные производные одной и той же функции, отличающиеся лишь порядком дифференцирования, равны между собой при условии их непрерывности.
Так, 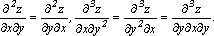
Пример. 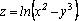 Показать, что
Показать, что 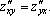
Решение.
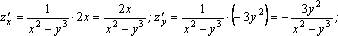
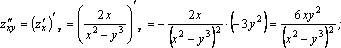
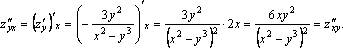
 2014-02-02
2014-02-02 400
400







