Пример 1

ОБЩАЯ СХЕМА ИССЛЕДОВАНИЯ.

Все выше приведенные шаги исследования поведения функции удобно выполнять по следующим этапам.

1. Исследуется сама функция у = у (х).

2. Исследуется первая производная у'.

3. Исследуется вторая производная у''.

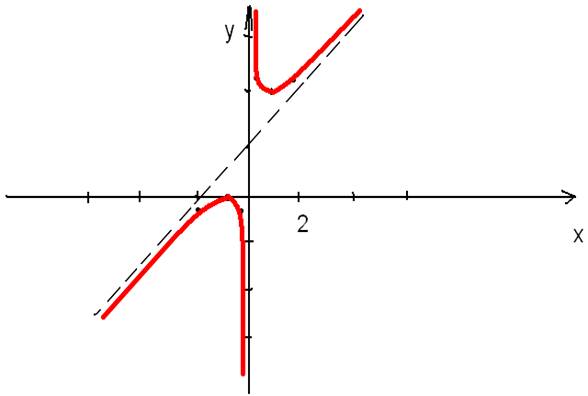
Исследуем поведение функции у = х + 2 + 1\х и построим ее график.

Решение:

1. Преобразуем функцию: у = х² + 2х + 1 п х. х

2. О.О.Ф.: вся ось Ох, кроме точки х = 0.

В окрестности точки х = 0 (в окрестности вертикальной асимптоты), функция ведет себя как 1\х, т.е. основным становится третье слагаемое в выражении для у.

Проверим наличие наклонных асимптот.

1 х2

2 х

Согласно (1) вычислим предел:

к = ℓim у(х) = ℓim х² + 2х + 1 = ℓim(1 + +)=1.

х→ - ∞ х х→ - ∞ х · х х→ - ∞

Аналогично найдем ℓim у(х) = 1.

х→ + ∞х

Таким образом, при х→ - ∞ и при х→ + ∞ функция имеет асимптоты.

Вычислим теперь свободный член в соответствии (1):

в = ℓim [у(х) – кх] = ℓim х² + 2х + 1 – 1 · х =

х→ - ∞ х→ - ∞ х

= ℓim (х + 2 + 1\х – х) = 2.

х→ - ∞

Аналогично найдем ℓim [у(х) – кх] = 2.

х→ + ∞

Следовательно, функция имеет общую наклонную асимптоту для х→ - ∞ и для х→ + ∞. Ее уравнение есть у = х + 2.

3. Никаким типом четности функция не обладает, она также непериодическая.

4. Корни функции найдем, решив уравнение х² + 2х + 1 = 0.

х

Числитель этого выражения, следовательно, и сама функция, имеет единственный кратный корень х = -1.

Рисуем систему координат и заносим на нее найденные асимптоты.

5. Выясним области знакопостоянства функции. Учтем, что для аргумента х найдено два характерных значения:

х = -1 – корень (кратный),

х = 0 – вертикальная асимптота.

Переходим к анализу первой производной.

1 х2

у' = 1 –.

Видим, что у' = 0 при х = ± 1. Эти две точки подозрительны на экстремум. Причем, у(-1) = 0, у(1) = 4.

Составим таблицу:

х	х < -1	-1	-1 < x < 0	0 < x < 1		х > 1
у'	+		-	-		+
у
		max			min

6. Исследуем поведение второй производной.

у'' = 2\х³.

Отсюда видим, что у'' < 0 при х < 0. Т.е. в области отрицательных значений аргумента график функции имеет выпуклость вверх (таблица 2).

Если х > 0, то у'' > 0. Теперь выпуклость обращена вниз.

7. Дополним таблицу данными второй производной и дополнительными точками из промежутков знакопостоянства.

х	х<-1	-1	-1<x<0	0<x<1		х>1	-2	-1\2	1\2
у'	+		-	-		+	3\4	-3	-3	3\4
у''							-	-	+	+
у							-1\2	-1\2	4,5	4,5
		max			min

8. Приступаем к построению графика функции…

асимптота у = х + 2

асимптота х = 0