Одноканальная СМО с ожиданием

На СМО поступает поток заявок с интенсивностью l, интенсивность обслуживания m (т.е. в среднем непрерывно занятый канал будет выдавать m обслуженных заявок в единицу времени), n=1. Заявка, поступившая в момент, когда канал занят, становится в очередь и ожидает обслуживания. Предположим, что количество мест в очереди ограничено числом m (в дальнейшем, при m®¥ можно получить характеристики одноканальной СМО без ограничений по длине очереди). Будем нумеровать состояния СМО по числу заявок, находящихся в системе (как обслуживаемых, так и ожидающих обслуживания):

S₀ – канал свободен; S₁ – канал занят, очереди нет; S₂ – канал занят, одна заявка стоит в очереди; S_k – канал занят, k -1 стоят в очереди; S_m₊₁ – канал занят, m заявок стоят в очереди. Граф состояний (размеченный) имеет вид:

Снова схема гибели и размножения. Пользуясь общим решением, напишем выражения предельных вероятностей состояния:

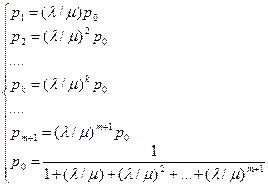или 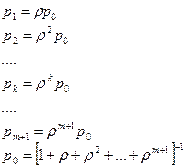(9.9).

В знаменателе выражения для р₀ стоит геометрическая прогрессия, суммируя её находим

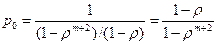(9.10).

(9.10) справедливо только при 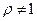(иначе неопределенность вида 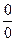). Но сумму геометрической прогрессии со знаменателем 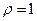найти ещё проще, чем по (9.10); она равна (m+2) и в этом случае p₀=1/(m+2) {то же самое получится, если раскрыть неопределенность по правилу Лапиталя}.

Определим характеристики СМО: Р_отк q, А, среднюю длину очереди 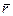, среднее число заявок, связанных с системой .

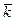Очевидно, заявка получает отказ только в том случае, когда канал занят и все m мест в очереди – тоже:

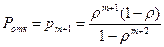(9.11).

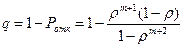(9.12).

А=lq. Найдем среднее число 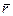, находящихся в очереди; определим эту величину как математическое ожидание дискретной случайной величины R – числа заявок, находящихся в очереди:.

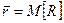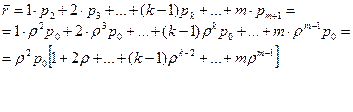Выведем формулу для суммы. Эта сумма не что иное, как производная по r суммы 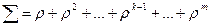, а для этого выражения мы можем воспользоваться формулой суммы геометрической прогрессии:

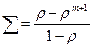
Продифференцируем её по r и проведя преобразования, найдем

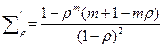(9.13).

Тогда .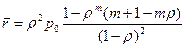

Подставляем p₀ из (10) и получаем

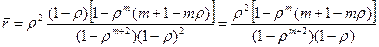(9.14).

Выведем теперь формулу для 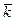. Рассмотрим общее число заявок К, связанных с системой, как сумму двух случайных величин: числа заявок, стоящих в очереди и числа заявок, находящихся под обслуживанием: .

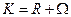По теореме сложения математических ожиданий:

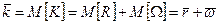, где 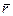- среднее число заявок в очереди; 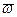- среднее число заявок под обслуживанием. Найдем 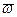. Т.к. канал у нас один, то случайная величина 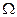может принимать только два значения: 0 или 1. Значение 0 она принимает, если канал свободен; вероятность этого равна 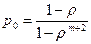. Значение 1 она принимает, если канал занят; вероятность этого равна .

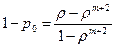Отсюда находим:

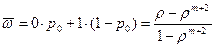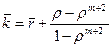, где 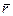находим из (9.14).

Выведем выражение еще для одной существенной характеристики СМО с ожиданием: среднего времени ожидания заявки в очереди. Обозначим его 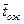. Пусть заявка приходит в систему в какой-то момент времени. С вероятностью p₀ канал обслуживания не будет занят и ей не придется стоять в очереди (t_ож=0). С вероятностью p₁ она придет в систему во время обслуживания какой-то заявки, но перед ней не будет очереди, и заявка будет ждать начала своего обслуживания в течение времени 1/m (среднее время обслуживания одной заявки). С вероятностью p₂ в очереди перед ней будет стоять еще одна заявка и время ожидания в среднем будет 2/m и т.д. Вообще, с вероятностью p_k пришедшая заявка застанет в системе k заявок и будет ждать в среднем k/m единиц времени (1£k£m). При k=m+1 (в очереди m заявок, вероятность этого p_m₊₁) t_ож=0 (заявка не обслуживается).

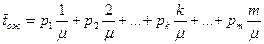Подставим сюда выражения для p₁,p₂,…p_m из (9.9).

Преобразуем сумму в скобках, используя (9.13)

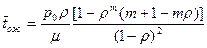
Или, выражая p₀ через r

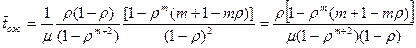Сравнивая это выражение с (9.14), замечаем, что

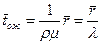, (9.15)

т.е. среднее время ожидания равно среднему числу заявок в очереди, деленному на интенсивность потока заявок.

Выведем ещё одну формулу для среднего времени пребывания заявки в системе. Обозначим случайную величину – время пребывания заявки в СМОчерез Т_сист _.. Она складывается из двух слагаемых (тоже случайных):

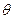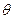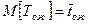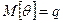
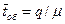Т_сист.=Т_ож+, где Т_ож - время ожидания заявки в очереди, случайная величина, равная времени обслуживания Т_об, если заявка обслуживается и 0, если она не обслуживается (получает отказ). По теореме сложения математических ожиданий: , но в наших обозначениях , а . Отсюда находим: 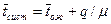или с учетом (9.15)

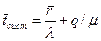Формула Литтла (первая): для любой СМО, при любом характере потока заявок, при любом распределении времени обслуживания, при любой дисциплине обслуживания среднее время пребывания заявки в системе равно среднему числу заявок в системе, деленному на интенсивность потока заявок.

Формула Литтла (вторая): для любой СМО, при любом характере потока заявок, при любом распределении времени обслуживания, при любой дисциплине обслуживания среднее время пребывания заявки в очереди равно среднему числу заявок в очереди, деленному на интенсивность потока заявок.

Теперь можно рассмотреть работу одноканальной СМО с ожиданием при m®¥ (неограниченная очередь). Совершить предельный переход m®¥. Можно рассмотреть работу многоканальной СМО с ожиданием. Состояние системы будем нумеровать по числу заявок, связанных с системой:

S₀ – все каналы свободны;

S₁ – занят один канал, остальные свободны;

… … …

S_k – заняты k каналов, остальные свободны;

… … …

S_n – заняты все n каналов;

S_n₊₁ – заняты все n каналов, одна заявка стоит в очереди;

… … …

S_n₊_r – заняты все n каналов, r заявок в очереди;

… … …

S_n₊_m – заняты все n каналов, m заявок в очереди.

Размеченный граф состояний имеет вид

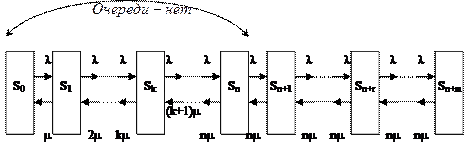Написать уравнения Колмогорова. Найти вероятности состояний. В их помощью рассчитать все интересующие величины. Затем опять можно рассмотреть и случай m®¥.

Можно рассмотреть СМО с ограниченным временем ожидания (на каждую заявку, стоящую в очереди действует как бы «поток уходов» с интенсивностью 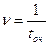(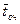- среднее время пребывания в очереди)).

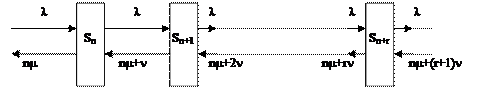Существуют и другие разновидности СМО: замкнутые СМО (интенсивность потока поступающих заявок зависит от состояния самой СМО), СМО с «взаимопомощью» между каналами (незанятые каналы «помогают» занятому в обслуживании).