Ускорение

Изменение модуля и направления вектора скорости описывается физической величиной, которая называется ускорением:

. (1.6)

Среднее ускорение за время определяется аналогично вектору средней скорости:

. (1.7)

Как и всякий вектор, ускорение можно записать в виде

.

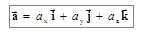Проекции и величина вектора ускорения вычисляются по формулам:

, , ,

.

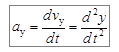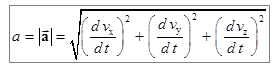Представим вектор скорости в виде , где v – модуль (величина) вектора скорости, а 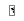– единичный вектор, направленный по касательной к траектории. В общем случае и величина и направление вектора скорости изменяются с течением времени, тогда согласно формуле (1.6) получаем

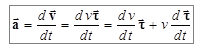. (1.8)

Первое слагаемое в выражении (1.8) характеризует изменение скорости по величине, и по направлению совпадает с направлением вектора скорости. Это слагаемое называется тангенциальным ускорением.

Рассмотрим второе слагаемое в (1.8). Вначале определимся с направлением. По мере того, как угол da будет стремиться к 0, вектор будет уменьшаться: и 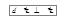. Таким образом, вектор, соответствующий второму слагаемому в формуле (1.8), перпендикулярен к касательной к траектории в данной точке. Поэтому второе слагаемое в формуле (1.8) называют нормальным ускорением, которое характеризует изменение вектора скорости по направлению (рис. 1.3).

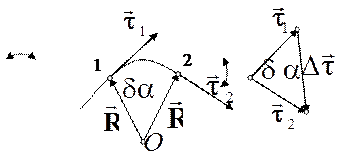
Рисунок 1.3 – Определение вектора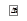

Таким образом, получаем, что

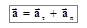. (1.9)

Теперь определим величину нормального ускорения. Можно записать, что

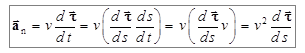. (1.10)

Можно строго показать, что при стремлении точки 2 к точке 1 (рис. 1.3) отрезок траектории между этими точками будет стремиться к дуге окружности некоторого радиуса R с центром в точке О. Точку О называют центром кривизны траектории, а радиус R называют радиусом кривизны траектории в данной точке. Из рисунка 1.3 видно, что

, или 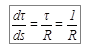. (1.11)

Теперь подставим выражение для 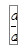из выражения (1.11) в выражение (1.10) и окончательно получим, что 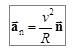. Здесь 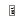– единичный вектор нормали к траектории в данной точке. Окончательно полное ускорение запишется в виде

. (1.12)

Модуль полного ускорения, как обычно, определяется следующим образом:

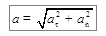. (1.13)

Можно показать, что всякое сложное движение можно свести к двум простым движениям – поступательному и вращательному. Мы, для простоты, как правило, будем рассматривать эти движения по отдельности. Итак, для прямолинейного движения . Если при этом ускорение не изменяется с течением времени, то такое движение называется равнопеременным.

Пример. Прямолинейное движение с постоянным ускорением. Так как в этом случае направление вектора не изменяется, то дальше значок вектора писать не будем, а будем рассматривать ускорение как алгебраическую величину: , откуда , или 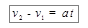. Здесь 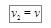– конечное значение скорости, а 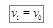– начальная скорость. С учётом сделанных замечаний окончательно получаем формулу

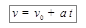. (1.14)

Проинтегрировав выражение (1.14) от 0 до некоторого t, найдём, что длина пути, пройденного за время t, определяется по известной школьной формуле

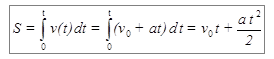. (1.15)