Радіус, діаметр і центр графа

Обчислення|підрахунок| відстаней і визначення маршрутів в графі є|з'являються,являються| одним з найбільш очевидних і практичних завдань|задач|, які виникають в теорії графів. Введемо|запровадимо| деякі необхідні визначення.

Ексцентриситет вершини графа – відстань до максимально віддаленої від неї вершини. Для графа, для якого не визначена вага його ребер, відстань визначається у вигляді числа ребер.

Радіус графа – мінімальний ексцентриситет вершин, а діаметр графа – максимальний ексцентриситет вершин.

Центр графа утворюють вершини, у|в,біля| яких ексцентриситет рівний радіусу. Центр графа може складатися з однієї, декількох або всіх вершин графа.

Периферійні вершини мають ексцентриситет, рівний діаметру.

Простий ланцюг|цеп| з|із| довжиною, рівною діаметру графа, називається діаметральною.

Теорема 12.1. У зв'язному графі діаметр не більше рангу його матриці суміжності.

Теорема 12.2. (Жордана|) Кожне дерево має центр, що складається з однієї або двох суміжних вершин.

Теорема 12.3. Якщо діаметр дерева парний, то дерево має єдиний центр, і всі діаметральні ланцюги|цепи| проходять через нього, якщо діаметр непарний, то центрів два і всі діаметральні ланцюги|цепи| містять|утримують| ребро, їх що сполучає|поєднує,з'єднує|.

Очевидно практичне значення центру графа. Якщо, наприклад, йдеться про графу доріг з|із| вершинами-містами, то в математичному центрі доцільно розміщувати адміністративний центр, складські приміщення|помешкання| і т.п. Цей же підхід можна застосовувати і для зваженого графа, де відстані – це ваги ребер. Як вагу можна брати евклидову| відстань, час або вартість пересування між пунктами.

Приклад|зразок| 12.5. Знайти радіус, діаметр і центр графа, зображеного|змальованого| на мал. 12.1.

Рішення|розв'язання,вирішення,розв'язування|. У даному завданні|задачі| зручно використовувати матрицю відстаней S. Елемент цієї квадратної симетричної матриці 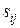рівний відстані між вершиною i і вершиною j. Для графа, показаного на мал. 12.1, матриця відстаней має наступний|слідуючий| вигляд|вид|:

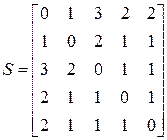. (12.2)

Обчислимо|обчислятимемо,вичислимо| ексцентриситет 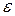кожної вершини. Цю величину можна визначити як максимальний елемент відповідного стовпця матриці відстаней (або рядки – оскільки матриця S симетрична). Одержуємо

|отримуємо|

№

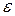Радіус графа r – мінімальний ексцентриситет вершин. В даному випадку r = 2. Такий ексцентриситет мають вершини № 2 № 4 і № 5. Ці вершини утворюють центр графа. Діаметр графа d – максимальний ексцентриситет вершин. В даному випадку d = 3. Такий ексцентриситет мають вершини № 1 і № 3, це периферія графа. У розглянутому графі вершини виявилися або центральними, або периферійними. У графах більшого порядку|ладу| існують і інші вершини.

Ексцентриситети вершин невеликого графа легко обчислювати|обчисляти,вичисляти| безпосереднім підрахунком по малюнку. Проте|однак| не завжди граф заданий своїм малюнком. Крім того, граф може мати великий розмір. Тому необхідний інший спосіб рішення попередньої задачі. Відома наступна|така| теорема.

Теорема 12.4. Хай|нехай| 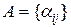– матриця суміжності графа G без петель і 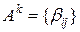, де 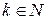. Тоді 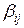рівно числу маршрутів довжини k від вершини 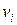до вершини .

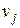Рішення задач теорії графів за допомогою різних перетворень матриці суміжності називають алгебраїчнимметодом.

Приклад|зразок| 12.6. Знайти матрицю відстаней графа, зображеного|змальованого| на мал. 12.1 алгебраїчним методом.

Рішення|розв'язання,вирішення,розв'язування|. Матриця суміжності даного графа рівна:

.

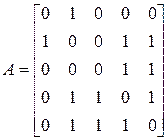Заповнюватимемо матрицю відстаней, розглядаючи|розглядуючи| ступені|міри| матриці суміжності. Одиниці матриці суміжності показують пари вершин, відстань між якими рівна одиниці (тобто вони сполучені|з'єднані| одним ребром).

.

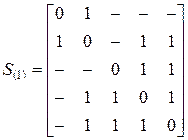Діагональні елементи матриці відстаней – нулі. Умножаємо|множимо| матрицю суміжності на себе:

.

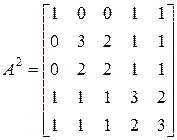Згідно теоремі між вершинами 2 і 3, 1 і 4 і т.д. є|наявний| деяке число маршрутів завдовжки 2 (оскільки ступінь|міра| матриці рівний двом). Число маршрутів тут не використовується, важливий|поважний| сам факт наявність маршруту і його довжина, на що і указує|вказує| ненульовий елемент ступеня|міри| матриці, не співпадаючий з|із| елементом, відміченим при обчисленні|підрахунку| маршруту меншої довжини. Проставляємо 2 в незаповнені елементи матриці відстаней і одержуємо|отримуємо| наступне|слідуюче| наближення:

.

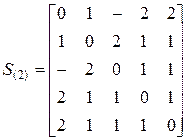Залишилося невідомим відстань між вершинами 1 і 3. Умножатимемо|множитимемо| матрицю суміжності саму на себе до тих пір, поки в матриці не з'явиться|появиться| ненульовий елемент 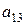. Тоді відповідний елемент матриці відстаней рівний ступеню|мірі| матриці суміжності: 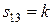. На наступному|такому| кроці одержуємо|отримуємо|

,

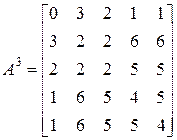отже, 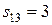, і остаточно

.

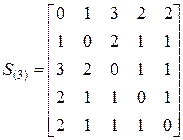Одержана|отримана| матриця співпадає|збігається| з|із| матрицею відстаней S (12.2), знайденою безпосередніми обчисленнями|підрахунками| по малюнку.

12.3. Ейлерів| ланцюг|цеп|

Маршрут в неографе|, в якому всі ребра різні, називається ланцюгом|цепом|. Ланцюг|цеп| в графі називається ейлеревим|, якщо він містить|утримує| всі ребра і всі вершини графа.

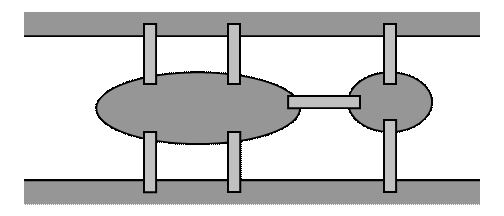
Мал. 12.4. Схема Кенігсбергськіх мостів

Теорія графів багато разів переоткрывалась різними авторами при рішенні різних прикладних задач. У їх ряду|лаві,низці| – знаменитий математик Леонард Ейлер| (1707-1783). До створення|створіння| теорії графів його підштовхнуло завдання|задача| про Кенігсберські мости, яке він вирішив|розв'язав| в 1736 році. По умові завдання|задачі| потрібно було пройти|минути,спливти| по всіх семи мостах міста Кенігсберга через річку|ріку| Преголь по одному разу і повернутися до початкової точки. На мал. 12.4 показана схема цих мостів (один з них сполучає|поєднує,з'єднує| між собою два острови, а інші – острови з|із| берегами). Цій схемі відповідає приведений на наступному|такому| малюнку мультиграф з|із| чотирма вершинами.

Мал. 12.5

Ейлер вирішив|розв'язав| завдання|задачу| про Кенігсбергські мости в негативному|заперечному| сенсі|змісті,рації|. Він довів, що дане завдання|задача| не має рішення|розв'язання,вирішення,розв'язування|. Для цього йому довелося|припало| довести наступну|таку| теорему.

Теорема 12.5 (Ейлера). Мультиграф володіє ейлеревим| ланцюгом|цепом| тоді і тільки|лише| тоді, коли він зв'язний і число вершин непарного ступеня|міри| рівне 0 або 2.

Вершини непарного ступеня|міри| в цій теоремі, очевидно, є|з'являються,являються| початком і кінцем ланцюга|цепу|. Якщо таких вершин немає, то ейлеревий| ланцюг|цеп| стає ейлеревим | циклом. Граф, що володіє ейлеревим| циклом, називається ейлеревим |. Якщо граф має ейлеревий| ланцюг|цеп|, але|та| не володіє ейлеревим| циклом (число вершин непарного ступеня|міри| рівне 2), то він називається полуейлеревим | графом.

Припустимо|передбачимо|, що граф має ейлерів| цикл. Рухаючись|сунучись| по ньому, підраховуватимемо|підсумовуватимемо| ступені|міри| вершин, вважаючи|гадаючи| їх до почала|розпочала,зачала| проходження нульовими. Проходження кожної вершини вносить 2 в ступінь|міру| цієї вершини. Оскільки ейлеревий| цикл містить|утримує| всі ребра, то коли обхід буде закінчений, буде враховані всі ребра, а ступені|міри| вершин – парні.

Всі чотири вершини мультиграфа, показаного на мал. 12.5, мають непарні ступені|міри|. Тому цей граф не володіє ейлеревим| циклом, а завдання|задача| про Кенігсбергськіх мости не має рішення|розв'язання,вирішення,розв'язування|.

Розглянемо|розгледимо| для порівняння граф, що володіє ейлеревим| ланцюгом|цепом|. У графі на мал. 12.6 тільки|лише| дві вершини мають непарний ступінь|міру|, отже, ейлеревий| ланцюг|цеп| є.

Мал. 12.6

Ланцюгів|цепів| може бути декілька. Наприклад, граф на мал. 12.6 має два ейлеревих| ланцюга|цепи|: 1-2-3-4-1-3 і 1-2-3-1-4-3.