Розкриття невизначеностей. Правило Лопіталя

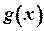Теорема 1 (правило Лопіталя). Нехай функції і визначені в проміжку 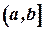і . Нехай, крім того, в проміжку 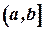існують скінченні похідн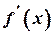і і , причому . Тоді, якщо існує границя , то існує й границя 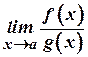, причому

.

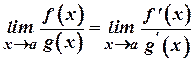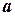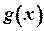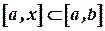Доведення. Доозначимо в точці функції і , поклавши . Тоді на відрізку функції і 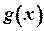задовольняють умовам теореми Коші. Отже,

,

де 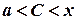. Якщо 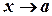, то зрозуміло, що й 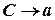. Враховуючи, що і те, що існує границя , робимо висновок

.

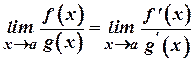Зауваження. Якщо похідні 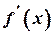і задовольняють умовам, котрі накладаються в наведеній теоремі на функції і 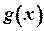, то правило Лопіталя можна застосувати повторно, тобто

.

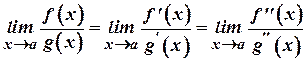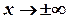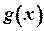Теорема 1 справджується й тоді, коли . Нехай функції і визначені в проміжку , , і в проміжку існують скінчені похідні 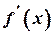та , де . Тоді, якщо існує границя 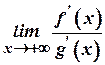, то існує й границя 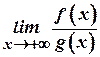, причому

.

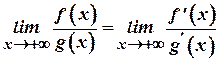Для доведення цього твердження достатньо покласти і застосувати теорему 1.

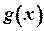Теорема 2 (правило Лопіталя). Нехай функції і визначені в проміжку 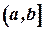, 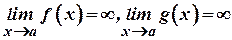і в проміжку 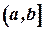існують скінчені похідні 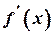та , причому . Тоді, якщо існує границя , то існує й границя 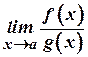, причому

.

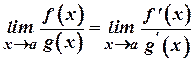Доведення цієї теореми можна прочитати, наприклад, в книзі Г. М. Фихтенгольца “Основы математического анализа”, т. 1. - М.: Наука, 1964. Теорема 2 має місце також, коли .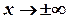

Правило Лопіталя дає можливість розкривати невизначеності типу .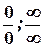

Приклади.

1.

2.