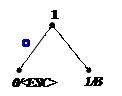
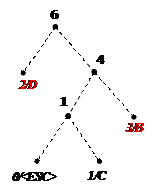
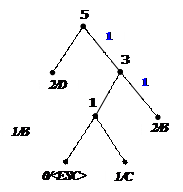
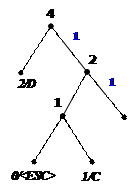
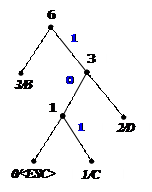
Процес декодування ілюструється таблицею 1, відповідні зміни кодового дерева – рис. 1.
 Таблиця 1
Таблиця 1
| Вхідний код | Символ | Довжина Коду | Номер дерева |
| ‘ B ’ | B | 1 | |
| 0‘ D ’ | D | 2 | |
| 00‘ C ’ | C | 3 | |
| D | 4 | ||
| B | 5 | ||
| B | 6 | ||
| C | 7 | ||
| B | 8 | ||
| C | 9 | ||
| D | 10 | ||
| C | 11 | ||
| D | 12 | ||
| B | 13 | ||
| B | 14 | ||
| D | |||
| å=53 |
1)
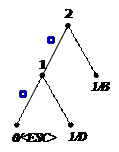
2)
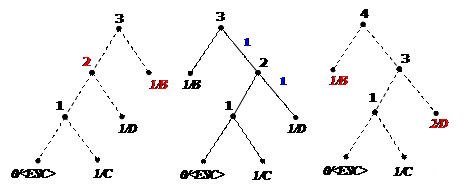
3) 4)
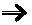 | |||||
 | |||||
 |
 5) 6)
5) 6)
 | |||||||
 | |||||||
 | 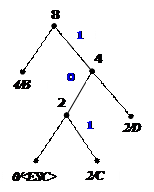 |
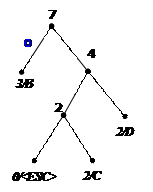
7) 8)
 | |||
 |
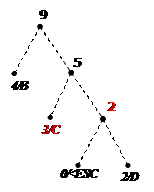

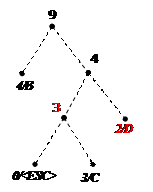
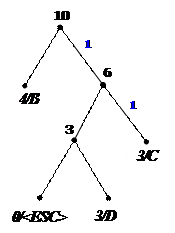 9)
9)
 |  |  |
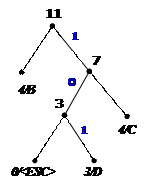
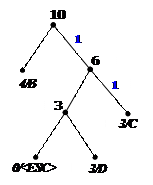
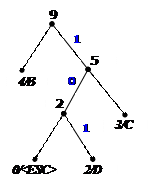 10) 11)
10) 11)

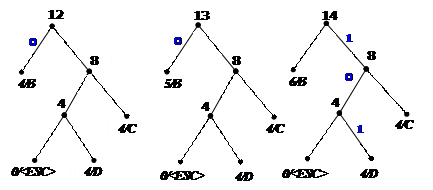 |
12) 13) 14)
|
Отже, закодоване повідомлення BDCDBBCBCDCDBBD.
Довжина стиснутого повідомлення L (X)= 53 (біти).
Довжина нестиснутого повідомлення в коді ASCII+
L (X)= 15×8=120 (бітів).
Задачі до розділу 6
1 Закодувати повідомлення AABCDAACCCCDBB за адаптивним алгоритмом Хаффмена. Обчислити довжину у бітах стиснутого повідомлення і його ASCII+ -коду.
2 Закодувати повідомлення КИБЕРНЕТИКИ за адаптивним алгоритмом Хаффмена. Обчислити довжини в бітах стиснутого повідомлення і його ASCII+ - коду.
3 Розкодувати повідомлення ‘ A ’0‘ F ’00‘ X ’01111101010110111101 00101, закодоване за адаптивним алгоритмом Хаффмена. Обчислити довжини кодів стиснутого і нестиснутого повідомлення в бітах.
4 Розкодувати повідомлення ‘D ’0‘ B ’0100‘ C ’000‘ A ’11010 11111110, закодоване за адаптивним алгоритмом Хаффмена. Обчислити довжини кодів стиснутого і нестиснутого повідомлення в бітах.
5 Закодувати повідомлення МАТЕМАТИКА за адаптивним алгоритмом Хаффмена. Обчислити довжини стиснутого повідомлення і вхідного повідомлення в коді ASCII+.
6 Розкодувати повідомлення ‘ B ’0‘ D ’00‘ C ’01111101010110111101 00101, закодоване за адаптивним алгоритмом Хаффмена. Обчислити довжини кодів стиснутого і нестиснутого повідомлення.
7 Розкодувати повідомлення ‘ К ’0‘ Р ’00‘ А ’100‘ С ’000‘ Н ’011100‘ Я ’ 0100‘ ’1100101001011110, закодоване за адаптивним алгоритмом Хаффмена. Обчислити довжини кодів стиснутого і нестиснутого повідомлення в бітах.
8 Закодувати повідомлення ПРОГРАММА за адаптивним алгоритмом Хаффмена. Обчислити довжини стиснутого повідомлення і вхідного повідомлення в коді ASCII+.
9 Закодувати повідомлення ТЕОРИЯ ИНФОРМАЦИИ за адаптивним алгоритмом Хаффмена. Обчислити довжини стиснутого повідомлення і вхідного повідомлення в коді ASCII+.
10 Розкодувати повідомлення ‘ В ’0‘ О ’00‘’100‘ Д ’1010000‘ Р ’0100‘ Е ’ 01011001010010000‘ Н ’10000‘ И ’111100‘ К ’, закодоване за адаптивним алгоритмом Хаффмена. Обчислити довжини кодів стиснутого і нестиснутого повідомлення.
11 Розкодувати повідомлення ‘ X ’0‘ F ’00‘ Z ’1111101100‘ A ’11101011, закодоване за адаптивним алгоритмом Хаффмена. Обчислити довжини кодів стиснутого і нестиснутого повідомлення.
[1] Шеннон К. Работы по теории информации и кибернетике. - М., Изд-во иностранной литературы, 1963.
[2] Фано Р. Передача інформації. Статистична теорія зв'язку. –М.:
Мир, 1965.
 2014-02-03
2014-02-03 275
275






