Лекция № 8 Понятие подстановки. Элементы алгебры подстановок. Использование подстановок в тайнописи

Цель: рассмотреть понятие подстановки, тождественной подстановки,

объяснить, как выполняются действия умножения подстановок, нахождения обратной подстановки,

перечислить свойства произведения подстановок,

рассмотреть понятия инверсии, четности-нечетности подстановок

показать, как подстановки применяются в тайнописи

Получил как-то Фома от одного из своих друзей телеграмму. Эта телеграмма была какой-то странной. Вот что в ней было написано: «йажзеирпончорс медж».

Сможете ли вы "прочитать" этот текст? Фома же, немного подумав, понял секрет этой телеграммы. Его приглашали в гости. Он решил ответить в том же духе. Сочинил ответную телеграмму и зашифровал ее таким же способом. Получилась запись из двух строк:

"приеду в субботу встречайте",

''етйачертсвутоббусвудеирп''.

После окончания шифровки Фома захотел всю свою переписку с другом вести только зашифрованными текстами, меняя время от времени способ шифровки. Поэтому он рьяно взялся за разработку метода шифрования.

Буквы исходного текста он решил заменять номерами позиций, которые занимают эти буквы. Вот какой список номеров получил Фома для телеграммы друга:

(1, 2, 3,..., 18).

Затем он заметил, что зашифрованный текст отличается от исходного только измененным порядком буки. Как изменяется порядок букв, легко увидеть с помощью тех же номеров позиций. Например, зашифрованный текст телеграммы друга Фома теперь смог представлять и виде списка:

(18, 17, 16,..., 3, 2, 1).

Сопоставление этих двух списков дает ключ к шиф­ровке текста:

.

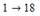
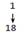Символьная запись читается так: «1 переходит в 18». Вместо нее часто используется другая запись:.

Направление стрелок определяет порядок шифровки текста. Например, буква, стоящая в шифруемом тексте в первой позиции, должна занять в зашифрованном тексте 18-ю позицию.

Если направление стрелок сменить на противоположное, то та же двухстрочная таблица будет определять порядок расшифровки текста. Например, буква, стоящая в зашифрованном тексте в 18-й позиции, должна занять в расшифрованном тексте первую позицию.

Наконец, если первая строка будет всегда связана с исходным текстом, то отпадет необходимость в использовании стрелок. (При шифровке исходным текстом является шифруемый текст, а при расшифровке – зашифрованный).

Поняв все это, Фома быстро записал ключ ко 2-ой шифровке своей телеграммы:

Осталось только сообщить каким-либо образом этот ключ своему другу, и тайна переписки гарантирована!

Если идеи Фомы вы поняли, то вот вам зашифрованное любимое его изречение:

"водянойпероревряй".

Оно зашифровано ключом:

Попробуйте-ка прочитать это изречение!

Решение

Ключ к шифровке:

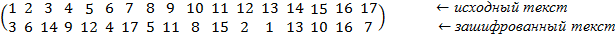
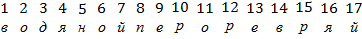
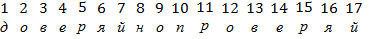
«Доверяй, но проверяй!»

Вы, вероятно, уже догадываетесь, что шифровальных ключей подобного вида можно придумать очень много. Каждый из них можно представить в виде двухстрочной таблицы:

.

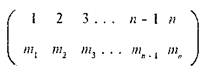Здесь в верхней строке стоят все натуральные числа от 1 до п в возрастающем порядке. Нижняя строка получается некоторой перестановкой чисел из верхней строки. Вся таблица в целом называется подстановкой порядка п.

Рассмотрим множество 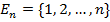, где 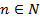, каждый элемент в которой представлен только один раз. Тогда взаимно-однозначное отображение множества 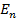на себя называется подстановкой степени п.

Множество подстановок п -й степени обозначается .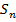

Отношение 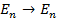бинарное, поэтому подстановки принято записывать в виде двухрядной матрицы, в первой строке которой записаны прообразы, а во второй – их образы:

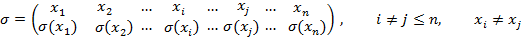
Если прообразы (аргументы) расположены в порядке возрастания (при 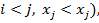то запись подстановки такого вида называют канонической. Если аргументы не записаны в порядке возрастания, то, переставляя столбцы (при этом сама подстановка не меняется, а изменяется лишь порядок произношения соответствий), можно верхнюю строку привести к упорядоченному виду:

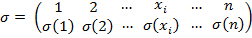или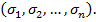

По возможности будем пользоваться именно канонической записью. Такая запись встречалась, когда мы записывали перестановку из п элементов. Отметим, что прообразом перестановки служит произвольное конечное множество, а прообразом подстановки – обязательно .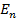

Найдем число возможных различных подстановок степени п. Поскольку каждой канонической записи подстановки эквивалентна соответствующая перестановка, то число подстановок п -й степени равна числу перестановок из п элементов, т. е. множество 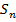состоит из 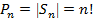элементов.

Вернемся к Фоме. С помощью подстановки-ключа

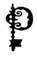
он зашифровал сообщение, состоящее из одного слова, и отправил его другу. Нерасшифрованное сообщение тот зашифровал еще раз, но уже с помощью другого ключа

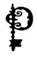
Получившееся дважды шифрованное сообщение он адресовал вам: "сноас".

Расшифруйте это сообщение. 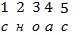, «сосна»

Процесс расшифровки вы можете провести значительно быстрее, если будете знать, как над подстановками выполняется одна алгебраическая операция. Эта операция называется умножением подстановок. (При желании вы можете назвать ее по-другому, ибо она никак не связана с обычным умножением чисел).

Рассмотрим на примере, как она выполняется. Умножим подстановки, с помощью которых шифровалось сообщение Фоме:

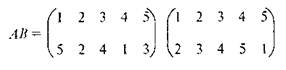
Процедура умножения сводится к последовательному проведению подстановок.

В первой подстановке (А): 1 → 5;

во второй подстановке (В): 5 → 1;

В итоге получаем: 1 → 1.

Аналогично, из "2 → 2" и "2 → 3" следует: "2 → 3". Проведя еще три рассуждения такого типа, получим подстановку-произведение

Используя подстановку АВ как шифратор, вы можете теперь в один прием расшифровать сообщение Фомы "сноас". Заодно проконтролируете себя.(ВА = «насос»)

Если вам будет интересно, то можете придумать свои подстановки-шифраторы сообщений и вести тайную переписку с друзьями.

Занимаясь расшифровкой сообщений, вы познакомились с алгебраической операцией над новыми объектами подстановками. Если кого-то из вас заинтересовали не только шифровки, но и сами по себе подстановки, то вы можете лучше познакомиться с ними, выполнив следующие задания.

ЗАДАНИЕ 1. Найдите произведения подстановок:

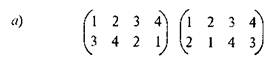
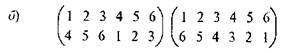
ЗАДАНИЕ 2. Найдите произведение ВА подстановок А и В, рассмотренных выше. Используя подстановку ВА как шифратор, расшифруйте еще раз сообщение "сноас". Сравните результат с результатом предыдущей расшифровки. После этого вы сможете сказать, обладает ли умножение подстановок свойством коммутативности.

Пусть заданы две подстановк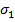и и 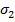, причем