Подстановкой n -ой степени называется взаимно однозначное отображение множества n элементов на себя.
Пример. Множество X ={ x 1, x 2, x 3} имеет 6 перестановок: x 1, x 2, x 3; x 1, x 3, x 2; x 2, x 1, x 3; x 2, x 3, x 1; x 3, x 1, x 2; x 3, x 2, x 1. Число возможных подстановок равно числу перестановок. Пусть запись 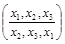 определяет одну из 6 возможных подстановок и означает, что x 1 переходит в x 2, x 2 переходит в x 3, x 3 переходит в x 1. Введем следующие обозначения для всех возможных подстановок:
определяет одну из 6 возможных подстановок и означает, что x 1 переходит в x 2, x 2 переходит в x 3, x 3 переходит в x 1. Введем следующие обозначения для всех возможных подстановок:
a = 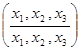 b =
b = 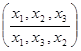 c =
c = 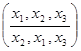
d = 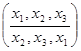 e =
e = 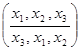 f =
f = 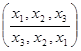
Введем операцию произведения (×) подстановок. Результатом произведения подстановок a и b является подстановка, получаемая в результате последовательного выполнения сначала подстановки a, а затем подстановки b. Например,
c × b = 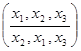 ×
× 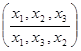 =
= 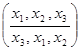 = e.
= e.
Результаты выполнения операции произведения подстановок 3-ей степени сведены в таблицу 1.1
Произведение подстановок ассоциативно, т.е. a´(b´j)=(a´b)´j, но не коммутативно a´b¹b´a (таблица, задающая операцию произведения подстановок, не симметрична относительно главной диагонали).
Подстановка 1= 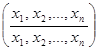 называется тождественной и играет роль единицы. Результатом произведения любой подстановки a на тождественную подстановку является подстановка a.
называется тождественной и играет роль единицы. Результатом произведения любой подстановки a на тождественную подстановку является подстановка a.
Таблица 1.1
Произведение подстановок
| a | b | c | d | e | f | |
| a | a | b | c | d | e | f |
| b | b | a | d | c | f | e |
| c | c | e | a | f | b | d |
| d | d | f | b | e | a | c |
| e | e | c | f | a | d | b |
| f | f | d | e | b | c | a |
Для любой подстановки a= 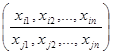 существует обратная подстановка a-1, получаемая из a путем перестановки строк - a-1=
существует обратная подстановка a-1, получаемая из a путем перестановки строк - a-1= 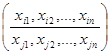 . Результатом произведения a´a-1=1 является тождественная подстановка (a´a-1=1).
. Результатом произведения a´a-1=1 является тождественная подстановка (a´a-1=1).
Итак, для оерации произведения подстановок n -ой степени (n ³3) выполняется (1), (3) и (4). При этом (2) не выполняется. Следовательно, алгебра, носителем которой является множество подстановок n -ой степени (n ³3), а сигнатура состоит из одной бинарной операции произведения подстановок, является группой.
 2015-04-01
2015-04-01 1992
1992
