Подстановки Эйлера

Интегралы вида.

Интегралы вида:

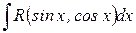
рационализируются подстановкой:

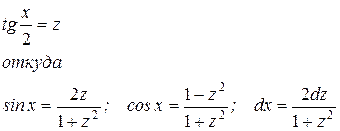
Пример 1:

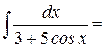
Пример 2:

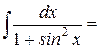
Интегралы вида:

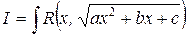
рационализируются одной из подстановок Эйлера:

Первая подстановка Эйлера применима при a >0:

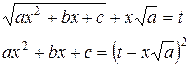
Члены, содержащие х ² взаимно уничтожаются, и х (а значит, и dx) выражается через t рационально.

Третья подстановка Эйлера применима всякий раз, когда трёхчлен 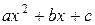имеет действительные корни, и, в частности, при a <0. Пусть корни будут х ₁ и х ₂, тогда полагаем

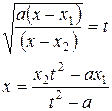
Рациональное выражение радикала находим так:

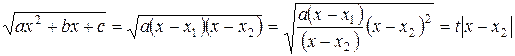
Замечание: первая и третья подстановки Эйлера достаточны, чтобы вычислить любой интеграл, рассматриваемого вида.

Вторая подстановка Эйлера применима при c >0:

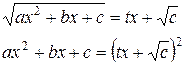
возводя в квадрат и деля затем на х, получаем рациональное выражение х через t.