Задача. Рама состоит из двух одинаковых частей 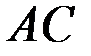 и
и 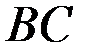 , соединённых между собой шарниром
, соединённых между собой шарниром 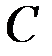 . Рама находится в равновесии под действием распределённой нагрузки, изменяющейся по закону треугольника (
. Рама находится в равновесии под действием распределённой нагрузки, изменяющейся по закону треугольника (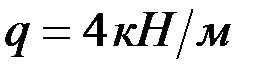 ), двух сил
), двух сил 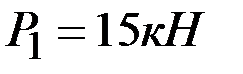 и
и 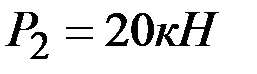 , приложенных в точках
, приложенных в точках 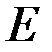 и
и 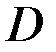 , пары с моментом
, пары с моментом 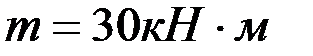 . Размеры указаны на рис. 66:
. Размеры указаны на рис. 66: 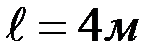 ;
; 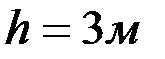 ;
; 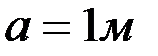 ;
; 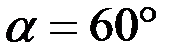 . Найти реакции опор
. Найти реакции опор 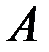 и
и 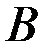 , а также реакцию шарнира
, а также реакцию шарнира 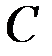 .
.
Рис. 66.
Решение. Рассматривается равновесие рамы, состоящей из двух жёстких частей 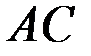 и
и 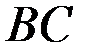 . Шарниры
. Шарниры 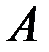 и
и 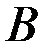 являются внешними связями, а шарнир
являются внешними связями, а шарнир 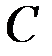 – внутренней связью.
– внутренней связью.
Решение задачи приведём двумя способами.
1. Рассмотрим равновесие всей рамы в целом, освободив её от внешних связей 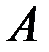 и
и 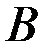 и заменив их действия соответствующими реакциями.
и заменив их действия соответствующими реакциями.
Направления реакций шарнирно неподвижных опор 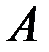 и
и 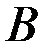 заранее неизвестны, поэтому их представляем составляющими
заранее неизвестны, поэтому их представляем составляющими 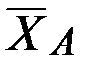 ,
, 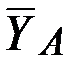 и
и 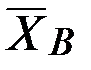 ,
, 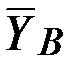 , направленными параллельно осям координат в сторону положительного отсчёта координат (рис. 67).
, направленными параллельно осям координат в сторону положительного отсчёта координат (рис. 67).
Распределённую нагрузку интенсивностью 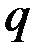 заменяем одной сосредоточенной силой
заменяем одной сосредоточенной силой  (равнодействующей распределённых сил), проходящей через центр тяжести треугольника. По модулю
(равнодействующей распределённых сил), проходящей через центр тяжести треугольника. По модулю 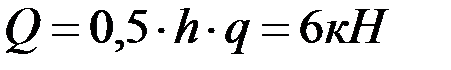 . Согласно аксиоме отвердевания система сил
. Согласно аксиоме отвердевания система сил 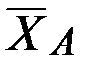 ,
, 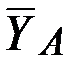 ,
, 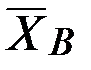 ,
, 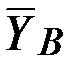 ,
,  ,
, 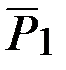 ,
, 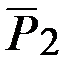 ,
, 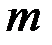 , действующих на раму, должна удовлетворять при её равновесии уравнениям равновесия твёрдого тела, хотя рама после освобождения от внешних связей (опор
, действующих на раму, должна удовлетворять при её равновесии уравнениям равновесия твёрдого тела, хотя рама после освобождения от внешних связей (опор 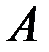 и
и 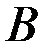 ) и не является жёсткой конструкцией.
) и не является жёсткой конструкцией.
Рис. 67.
Рассматриваемая система сил является плоской, уравнения равновесия составим по второй форме, вычисляя моменты сил относительно точек 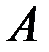 и
и 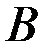 и проекции сил на ось
и проекции сил на ось 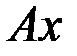 . Тогда в каждое уравнение войдёт наименьшее число неизвестных реакций.
. Тогда в каждое уравнение войдёт наименьшее число неизвестных реакций.
Для облегчения вычисления моментов силу 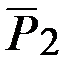 разложим на её составляющие
разложим на её составляющие 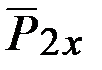 и
и 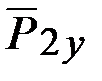 , и воспользуемся теоремой Вариньона о моменте равнодействующей силы. Учитывая, что
, и воспользуемся теоремой Вариньона о моменте равнодействующей силы. Учитывая, что 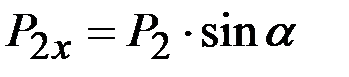 ,
, 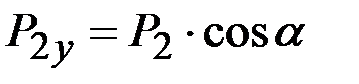 , получим уравнения равновесия всей конструкции в целом:
, получим уравнения равновесия всей конструкции в целом:
(39)
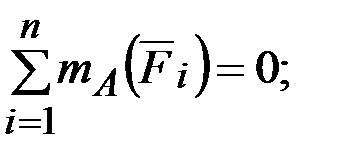
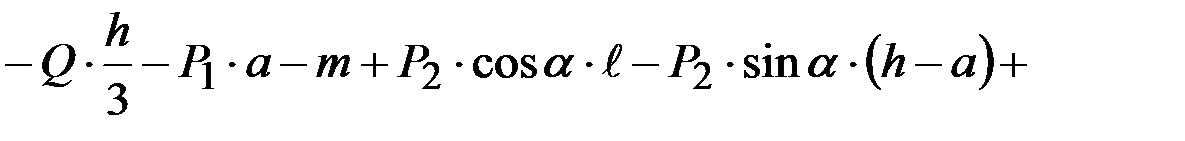
(40)
(41)
Во избежание пропусков рекомендуется при составлении уравнений равновесия силы перебирать в определённом порядке, например, идя слева направо.
Из уравнения (40) можно найти реакцию 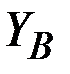 , из уравнения (41) – реакцию
, из уравнения (41) – реакцию 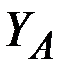 . Уравнение (39) содержит два неизвестных
. Уравнение (39) содержит два неизвестных 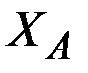 и
и 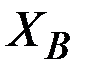 и не позволяет найти их значения, поэтому расчленим конструкцию по шарниру
и не позволяет найти их значения, поэтому расчленим конструкцию по шарниру 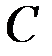 и рассмотрим дополнительно равновесие какой-либо одной части. Рекомендуется выбирать ту часть, к которой приложена наиболее простая система сил. В данной задаче удобнее рассматривать часть
и рассмотрим дополнительно равновесие какой-либо одной части. Рекомендуется выбирать ту часть, к которой приложена наиболее простая система сил. В данной задаче удобнее рассматривать часть 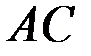 (рис. 68).
(рис. 68).
Рис. 68.
Отбрасываем вторую часть конструкции 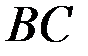 . Заменяем действие
. Заменяем действие 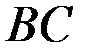 на первую часть конструкции соответствующей внутренней реакцией
на первую часть конструкции соответствующей внутренней реакцией 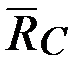 . Направление этой реакции, передаваемой через цилиндрический шарнир
. Направление этой реакции, передаваемой через цилиндрический шарнир 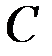 , неизвестно, поэтому изобразим её двумя составляющими
, неизвестно, поэтому изобразим её двумя составляющими 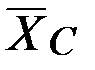 и
и 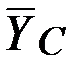 (рис. 68).
(рис. 68).
Уравнения равновесия части 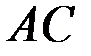 конструкции составим в первой форме:
конструкции составим в первой форме:
(42)
(43)
(44)
В результате подстановки числовых данных в (39) – (44) получим систему шести независимых уравнений для определения шести неизвестных 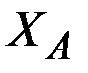 ,
, 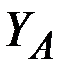 ,
, 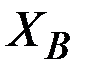 ,
, 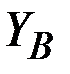 ,
, 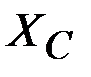 ,
, 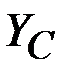 :
:
(45)
(46)
(47)
(48)
(49)
(50)
Решая систему уравнений (45) – (50), находим:
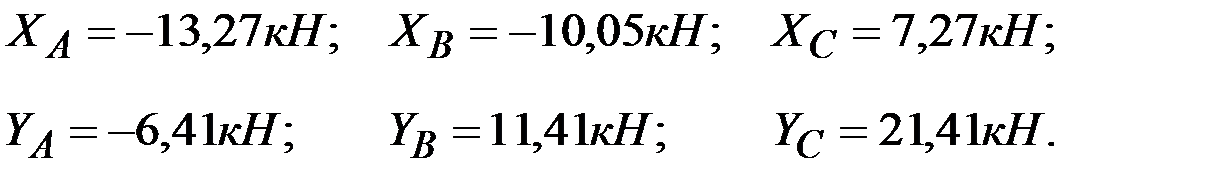
В действительности силы 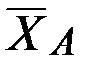 ,
, 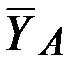 ,
, 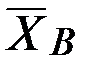 направлены в стороны, противоположные показанным на рис. 67 и 68.
направлены в стороны, противоположные показанным на рис. 67 и 68.
2. Решим эту же задачу вторым способом, расчленяя конструкцию на две части по шарниру 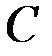 и рассматривая равновесие каждой части в отдельности с учётом взаимодействия этих частей (рис. 68).
и рассматривая равновесие каждой части в отдельности с учётом взаимодействия этих частей (рис. 68).
Уравнения равновесия части 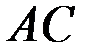 уже были составлены. Составим уравнения равновесия части
уже были составлены. Составим уравнения равновесия части 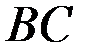 в первой форме:
в первой форме:
(51)
(52)
(53)
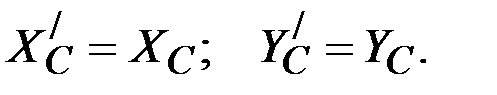
Заметим, что из векторного условия равенства действия и противодействия следует
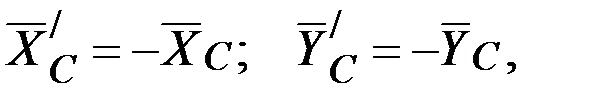
и не следует, что 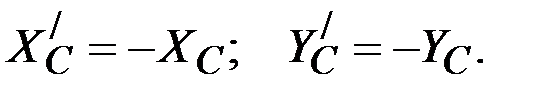
Убрав штрихи при неизвестных в уравнениях (51) – (53) и подставив числовые данные, получим
(54)
(55)
(56)
Последняя система уравнений (54) – (56) совместно с уравнениями (48) – (50) образует систему шести независимых уравнений для определения шести неизвестных. Решение этой системы будет точно таким же, как и решение, полученное способом 1.
Выбор способа решения зависит от характера задачи и определяется сложностью системы уравнений равновесия. Если система уравнений, полученная способом 1, окажется сложной, можно попытаться применить способ 2 решения задачи.
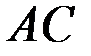 и
и 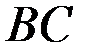 , соединённых между собой шарниром
, соединённых между собой шарниром 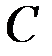 . Рама находится в равновесии под действием распределённой нагрузки, изменяющейся по закону треугольника (
. Рама находится в равновесии под действием распределённой нагрузки, изменяющейся по закону треугольника (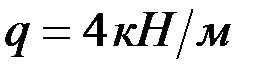 ), двух сил
), двух сил 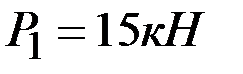 и
и 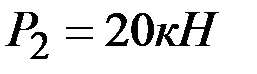 , приложенных в точках
, приложенных в точках 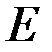 и
и 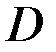 , пары с моментом
, пары с моментом 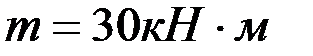 . Размеры указаны на рис. 66:
. Размеры указаны на рис. 66: 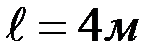 ;
; 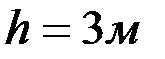 ;
; 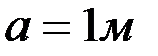 ;
; 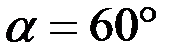 . Найти реакции опор
. Найти реакции опор 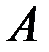 и
и 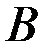 , а также реакцию шарнира
, а также реакцию шарнира 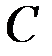 .
.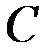
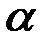
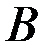
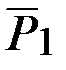
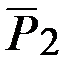
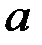
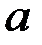
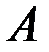
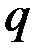
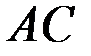 и
и 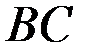 . Шарниры
. Шарниры 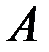 и
и 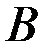 являются внешними связями, а шарнир
являются внешними связями, а шарнир 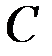 – внутренней связью.
– внутренней связью.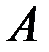 и
и 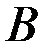 и заменив их действия соответствующими реакциями.
и заменив их действия соответствующими реакциями.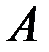 и
и 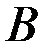 заранее неизвестны, поэтому их представляем составляющими
заранее неизвестны, поэтому их представляем составляющими 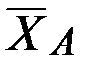 ,
, 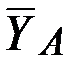 и
и 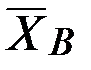 ,
, 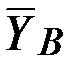 , направленными параллельно осям координат в сторону положительного отсчёта координат (рис. 67).
, направленными параллельно осям координат в сторону положительного отсчёта координат (рис. 67).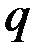 заменяем одной сосредоточенной силой
заменяем одной сосредоточенной силой  (равнодействующей распределённых сил), проходящей через центр тяжести треугольника. По модулю
(равнодействующей распределённых сил), проходящей через центр тяжести треугольника. По модулю 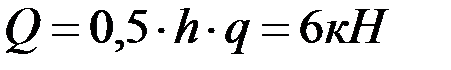 . Согласно аксиоме отвердевания система сил
. Согласно аксиоме отвердевания система сил 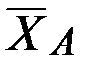 ,
, 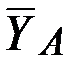 ,
, 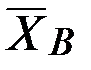 ,
, 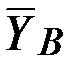 ,
,  ,
, 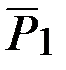 ,
, 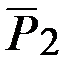 ,
, 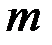 , действующих на раму, должна удовлетворять при её равновесии уравнениям равновесия твёрдого тела, хотя рама после освобождения от внешних связей (опор
, действующих на раму, должна удовлетворять при её равновесии уравнениям равновесия твёрдого тела, хотя рама после освобождения от внешних связей (опор 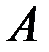 и
и 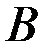 ) и не является жёсткой конструкцией.
) и не является жёсткой конструкцией.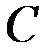
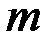
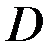
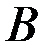
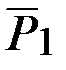
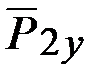
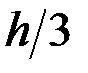

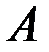
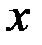
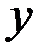
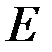
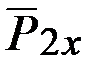
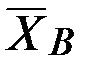
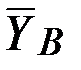
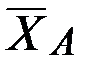
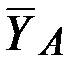
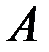 и
и 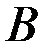 и проекции сил на ось
и проекции сил на ось 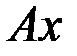 . Тогда в каждое уравнение войдёт наименьшее число неизвестных реакций.
. Тогда в каждое уравнение войдёт наименьшее число неизвестных реакций.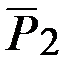 разложим на её составляющие
разложим на её составляющие 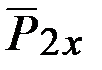 и
и 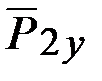 , и воспользуемся теоремой Вариньона о моменте равнодействующей силы. Учитывая, что
, и воспользуемся теоремой Вариньона о моменте равнодействующей силы. Учитывая, что 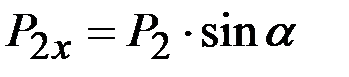 ,
, 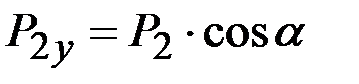 , получим уравнения равновесия всей конструкции в целом:
, получим уравнения равновесия всей конструкции в целом: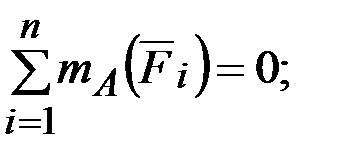
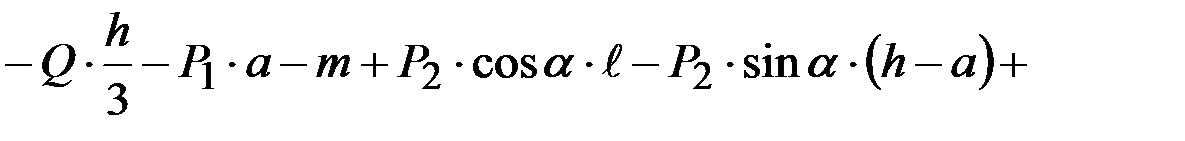
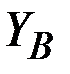 , из уравнения (41) – реакцию
, из уравнения (41) – реакцию 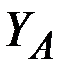 . Уравнение (39) содержит два неизвестных
. Уравнение (39) содержит два неизвестных 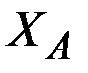 и
и 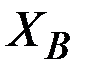 и не позволяет найти их значения, поэтому расчленим конструкцию по шарниру
и не позволяет найти их значения, поэтому расчленим конструкцию по шарниру 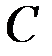 и рассмотрим дополнительно равновесие какой-либо одной части. Рекомендуется выбирать ту часть, к которой приложена наиболее простая система сил. В данной задаче удобнее рассматривать часть
и рассмотрим дополнительно равновесие какой-либо одной части. Рекомендуется выбирать ту часть, к которой приложена наиболее простая система сил. В данной задаче удобнее рассматривать часть 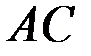 (рис. 68).
(рис. 68).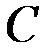
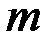
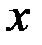
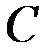
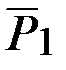
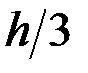

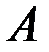
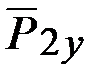
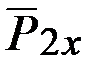
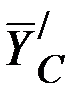
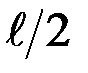
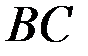 . Заменяем действие
. Заменяем действие 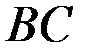 на первую часть конструкции соответствующей внутренней реакцией
на первую часть конструкции соответствующей внутренней реакцией 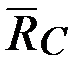 . Направление этой реакции, передаваемой через цилиндрический шарнир
. Направление этой реакции, передаваемой через цилиндрический шарнир 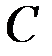 , неизвестно, поэтому изобразим её двумя составляющими
, неизвестно, поэтому изобразим её двумя составляющими 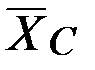 и
и 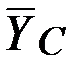 (рис. 68).
(рис. 68).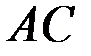 конструкции составим в первой форме:
конструкции составим в первой форме: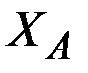 ,
, 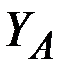 ,
, 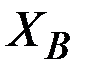 ,
, 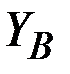 ,
, 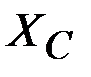 ,
, 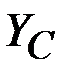 :
: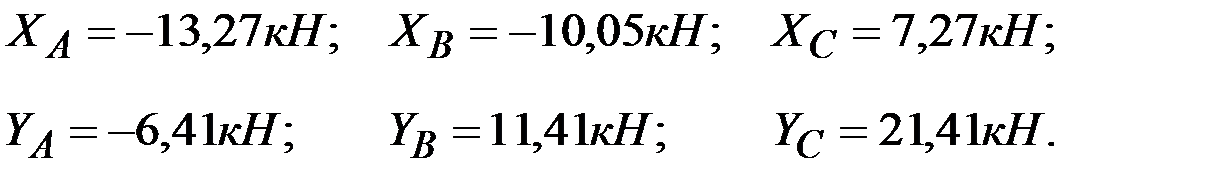
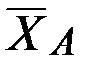 ,
, 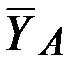 ,
, 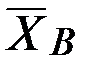 направлены в стороны, противоположные показанным на рис. 67 и 68.
направлены в стороны, противоположные показанным на рис. 67 и 68.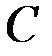 и рассматривая равновесие каждой части в отдельности с учётом взаимодействия этих частей (рис. 68).
и рассматривая равновесие каждой части в отдельности с учётом взаимодействия этих частей (рис. 68).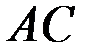 уже были составлены. Составим уравнения равновесия части
уже были составлены. Составим уравнения равновесия части 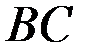 в первой форме:
в первой форме: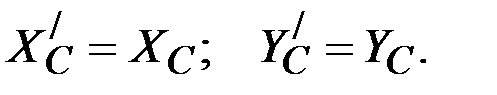
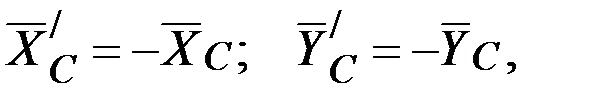
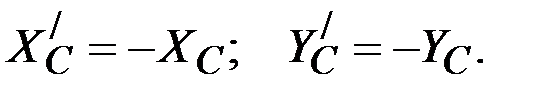
 2021-11-13
2021-11-13 241
241






