Алгоритмы. И что такое алгоритм

Алгоритм является последовательностью действий, совершение которых приводит к некоторому желаемому результату. В силу такого общего определения алгоритмы должны встречаться повсюду, что мы и наблюдаем в науке, искусстве, математике и других сферах деятельности человека. Далее будут приведены соответствующие примеры, но пока обратим внимание на следующее – представляя строго определённую последовательность действий, алгоритм зачастую может быть реализован физическим устройством, компьютером. Распространённость алгоритмов и возможность их реализации компьютером способны объяснить сегодняшнее повсеместное использование компьютеров. С другой стороны, осознание того, какие задачи не могут быть решены алгоритмически (а точнее имеют лишь частичное алгоритмическое решение – см. далее) позволяет понять, в каких случаях компьютер не до конца может справиться с поставленной задачей.

С точки зрения алгоритмической разрешимости естественно выделить следующие два типа практических задач, первый из которых является частным случаем второго:

1. Разрешимые задачи [существует алгоритм, возвращающий нужный результат на каждом наборе входных данных]

2. Частично разрешимые задачи [все практические задачи; существует алгоритм, возвращающий нужный результат, возможно, не на каждом наборе входных данных]

Обращаясь к первой теореме Гёделя (о неполноте формальной арифметики), мы покажем, что задачи типа 2 не исчерпываются задачами типа 1, т.е. существуют частично разрешимые задачи, не являющиеся разрешимыми. Начнём, впрочем, с рассмотрения разрешимых задач.

Решение квадратного уравнения. В школе было показано, как, используя дискриминант (или теорему Виета), можно найти корни квадратного уравнения (или показать, что таковых не существует). Данная задача разрешима на каждом наборе входных данных, т.е. при любых значениях коэффициентов a, b и c (a ≠ 0).

Изображение органического соединения. Не составляет труда проверить, соответствует ли заданное изображение (мультиграф) некоторой молекуле, содержащей водород, кислород, азот и углерод с валентностями 1, 2, 3 и 4, соответственно. Мультиграф будет задавать молекулу соединения тогда и только тогда, когда он связен (любые две вершины соединены путём), а его степени (число инцидентных вершинам рёбер) принимают значения 1, 2, 3 или 4. Пример мультиграфа, для которого соответствующий алгоритм вернёт значение “является молекулой”:

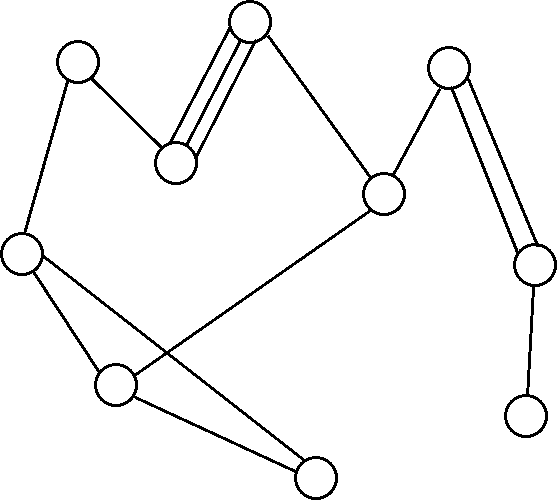
Приведённые примеры наводят на мысль о том, что большинство изучаемых в школе задач могло быть описано алгоритмически, а точнее – что эти задачи относятся к типу 1. Это предположение порой заставляет возмущаться учителями, которые не предоставляют соответствующих алгоритмов, т.е., получается, не окончательно знакомят учеников с предметом. В самом деле, почему бы не научить человека раз и навсегда грамотно писать, доказывать теоремы, сочинять стихи, музыку, рисовать? Мысль о “плохих учителях” подкрепляется и тем, что соответствующие задачи очевидным образом имеют частичное решение. Скажем, для некоторых поэтических “произведений” мы можем сразу сказать, что стихами они не являются, поскольку в них нет рифмы. Но следует ли, с другой стороны, из наличия рифмы в произведении то, что перед нами стихотворение? Вопрос, разумеется, риторический. То же касается музыки и изобразительного искусства: соответствие правилам музыкальной или графической композиции ещё не означает произведения искусства (возможно, этим можно объяснить, что людей, разбирающихся в той или иной области, больше, чем тех, кто эту область непосредственно творчески представляет). Таким образом, лишь для части антипроизведений (из области музыки, литературы, изобразительного искусства и др.) можно точно сказать – имеем ли мы действительно дело с антипроизведением, т.е. верно ли то, что рассматриваемый объект произведением не является. Соответствующие задачи относятся, стало быть, к задачам типа 2, и неизвестно, может ли им быть присвоен тип 1 в принципе.

Перейдём, наконец, к задаче, отсутствие полной разрешимости которой может быть строго доказано. По существу, соответствующее доказательство основывается на ограничении единственным алгоритмом и установлении того, что данный алгоритм работает не на всех входных данных. Речь идёт об определении истинностных значений арифметических утверждений. Так, мы можем с лёгкостью установить, какое из следующих утверждений истинно, а какое ложно:

1. Для каждого числа x найдётся число y, большее числа x на 1

2. Существует такое число x, которое больше каждого числа y

Интуитивные посылки, позволяющие определить истинность этих высказываний, могут быть формализованы. Иными словами, рассуждая, мы следуем здесь вполне определённому алгоритму F. Далее же можно обратиться к первой теореме Гёделя, в соответствии с которой существует такое утверждение из арифметики, истинностное значение которого с помощью F определено быть не может.