Реактивный стержень в прямоугольном волноводе

17.2. Диафрагмы. Тонкие металлические пластины. Применение

 

17 .2. Диафрагмы

Диафрагмами называют тонкие металлические пластины, введенные перпендикулярно оси линии передачи и перекрывающие часть поперечного сечения линии. Диафрагмы широко применяются как согласующие устройства, элементы связи в объемных резонаторах, в фильтрах, замедляющих структурах и других устройствах. На рис. 17.2.1-17.2.3 показаны диафрагмы в прямоугольном волноводе.

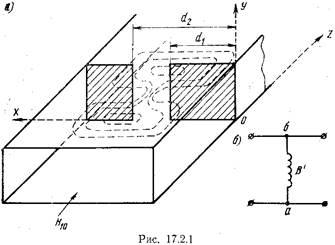
Совместим плоскость ху декартовой системы координат с металлическими пластинами диафрагмы, изображенной на рис. 17.2.1, и предположим, что-падающая на диафрагму волна 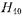 единичной амплитуды распространяется по волноводу слева направо. У волны  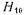составляющие электрического и магнитного полей не зависят от координаты у. Введение ин дуктивной диафрагмы не нарушает регулярности волновода вдоль этой оси. Поэтому все составляющие электромагнитного поля, образующиеся в результате дифракции волны  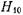на диафрагме, не должны зависеть от координаты у, т. е. ближнее поле описывается суперпозицией волн типа  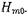Отсутствие вариаций поля по координате у предопределяет невозможность возбуждения волн .

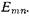В отрезке волновода до диафрагмы 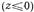 полное поле состоит из падающей волны  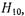отраженной волны того же типа,и бесконечного числа волн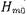 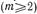 высшего типа с экспоненциально убывающей по мере удаления от диафрагмы амплитудой. Поэтому если обозначить через р - амплитуду отраженной волны  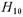и через  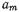- амплитуды волн высшего типа, то при  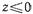составляющие  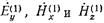полного поля в волноводе можно записать в виде:

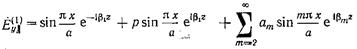 . (17.2.1)

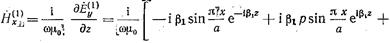
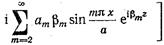;  (17.2.2)

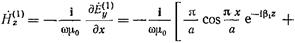
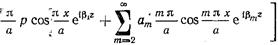, (17.2.3)

где 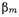 - коэффициент распространения волны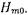  

Зависимость.между 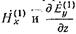, а также между  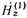и 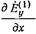следует из ур-ний (2.2.7) и (1.2.25), если учесть, что у волн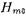 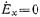и .

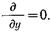В волноводе за диафрагмой распространяются прошедшая волна 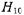с амплитудой t и бесконечное число волн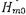 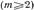с экспоненциально убывающей амплитудой. Поэтому при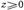

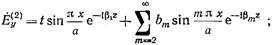 (17.2.4)  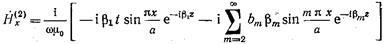(17.2.5)

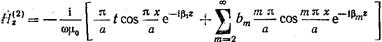 . (17.2.6)

В сечении z = 0, где расположена диафрагма, должны выполняться следующие граничные условия:

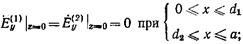 (17.2.7)  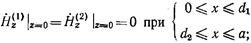(17.2.8)

 (17.2.9) 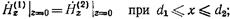 (17.2.10)  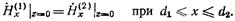(17.2.11)

Равенства (17.2.7) и (17.2.8) вытекают из условия обращения в нуль на металле диафрагмы касательной составляющей электрического поля и нормальной составляющей магнитного толя, а соотношения (17.2.9)-(17.2.11) получены из условия, что касательная и нормальная составляющие поля должны быть непрерывны во всех точках, где нет металла, т. е. на отверстии диафрагмы. Обозначим через 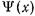 функцию, описывающую неизвестное пока распределение электрического поля в плоскости диафрагмы, т. е. положим 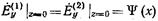при .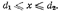

Так как 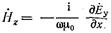, то граничные условия (17.2.8) и (17.2.10) можно записать в виде одного равенства

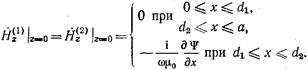 (17.2.12)

Подставляя в (17.2.12) ряд (17.2.3), получаем при z=0

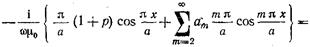
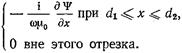 (17.2.13)

После умножения обеих частей равенства (17.2,13) на 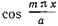 и почленного интегрирования в (пределах от нуля до а находим:  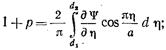(17.2. 14)  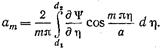(17.2.15)

В ф-лах (17.2.14) и (17.2.15) буква х заменена буквой 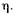 После подстановки (17.2.6) в (17.2.12), вычисления коэффициента и сравнения величин t и 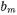с (17.2.14) и (17.2.15) имеем  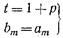. (17.2.16

Подставив в (17.2.2) и (17.2.5) вместо 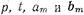их выражения

(17.2.14), (17.2.15) и (17.2.16) и приравняв в соответствии с граничным условием (17.2.11) полученные ряды, приходим к равенству

Поскольку волновод является предельным для всех волн, начиная с 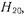 то можно принять при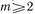  

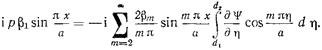 (17.2.17)  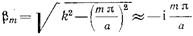(17.2.18)

Допустимость этого приближения нетрудно проверить прямым подсчетом. Если 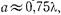 то наибольшая погрешность, порядка 30%, возникает при т=2. По мере увеличения индекса т погрешность приближенного равенства (17.2.18) быстро падает. Выбор отрицательного значения корня в (17.2.18), как можно заметить, обратившись к (17.2.1) - (17.2.6), обеспечивает экспоненциальное убывание амплитуды волн высших типов. Заменив в (17.2.17) величину  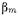в соответствии с (17.2.18), приходим к равенству

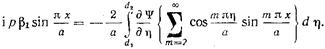 (17.2.19)

Сумма бесконечного ряда, стоящего под интегралом в (17.2.19), может быть найдена как предел суммы вида

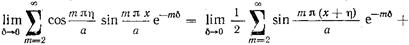
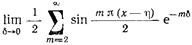. (17.2.20)

Если синусы в (17.2.20) заменить по формуле Эйлера 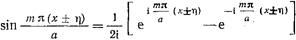 , (17.2.21)

то каждый из бесконечных рядов в (17.2.20) распадется на две сходящиеся геометрические прогрессия со знаменателем 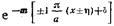 Суммируя по известной формуле эти геометрические прогрессии, и переходя к пределу 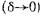, получаем после несложных тригонометрических преобразований

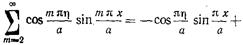
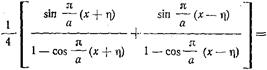
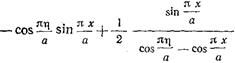
(17.2.22) что позволяет записать равенство (17.2.19) в виде

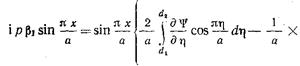
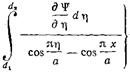. (17.2.23)

Первое слагаемое в фигурных скобках правой части (17. 2.23) согласно (17.2.14) равно 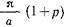. Поэтому после сокращения множителя  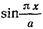в обеих частях равенства (17.2.23) получаем

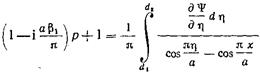 (17.2.24)

Чтобы упростить дальнейшие преобразования, выполним в (17.2.24) замену переменных вида

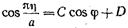 (17.2.25)

и подберем константы С и D так, чтобы интервал интегрирования (d₁, d₂) в (17.2.24) преобразовался в интервал 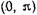, т.е. 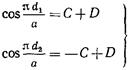, (17.2.26)

откуда 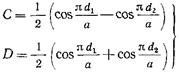 (17.2.27)

Так как 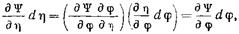  (17.2.28) то после подстановки (17.2.25) в (17,2.24) получаем

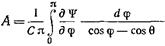 , (17.2.29) где приняты обозначения:

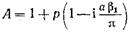
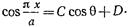   (17.2.30)

Искомая функция 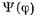 входит в (17.2.29) под знак интеграла, т. е. равенство (17.2.29) является интегральным уравнением. Согласно (17.2.11) функция  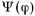описывает распределение электрического поля в отверстии диафрагмы. В соответствии с граничным условием (17.2.7) напряженность электрического поля на краях диафрагмы равна нулю, т. е. в новых переменных  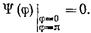(17.2.31)

Граничные условия (17.2.31) удовлетворяются, если предположить, что 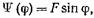 (17.2.32)

где F - константа, подлежащая определению. Подставляя (17.2.32) в (17.2.29), вычисляя интеграл и подставляя пределы, получаем 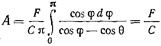 (17.2.33)

откуда F=AC и функция 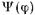равна 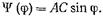 (17.2.34)

Можно доказать, что интегральное ур-ние (17.2.29) других решений не имеет.

Для определения коэффициента отражения р подставим (17.2.34) в (17.2.14). Тогда с учетом равенств (17.2.25) и (17.2.28)1 получаем 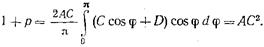 (17.2.35)

Подставляя в (17.2.35) вместо А его значение из (17.2.30), приходим к выражению 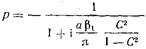 (17.2.36)

Нормированная проводимость в сечении 2-0 согласно (16.3.10) и (17.2.36) равна 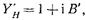 (17.2.37)

где 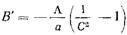 (17.2.38)

Так как согласно (17.2.27) С<1 при любых 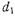 и 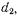 то реактивная проводимость всегда отрицательна. Следовательно, введение а прямоугольный волновод диафрагмы, изображенной на рис. 17.2.1а, соответствует согласно (17.2.37) включению в эквивалентную длинную линию параллельной индуктивности (рис. 17.2.16). Поэтому такую диафрагму называют индуктивной. Полученный результат можно пояснить следующим образом.

Реактивная проводимость любого элемента, в котором концентрируется энергия электрического поля 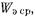 независимо от конструкции, носит емкостный характер. Реактивная проводимость любого элемента, в котором концентрируется энергия магнитного поля  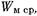носит индуктивный характер. Если концентрируется как электрическая, так и магнитная энергия, то характер проводимости зависит от соотношения между величинами  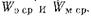Когда 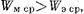 то проводимость носит индуктивный характер; когда  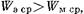то - емкостный характер; когда  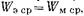то - чисто активный. Вблизи диафрагмы, как было показано выше, реактивное поле образуется нераспространяющимися волнами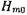 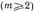  ). Используя выражения (14.1.23) и (14.1.24) для составляющих поля, можно показать, что у нераепространяющих-ся волн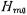 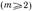 энергия, запасенная в магнитном поле, превышает энергию, запасенную в электрическом поле. Поэтому вблизи диафрагмы  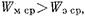что и определяет индуктивный характер ее проводимости.

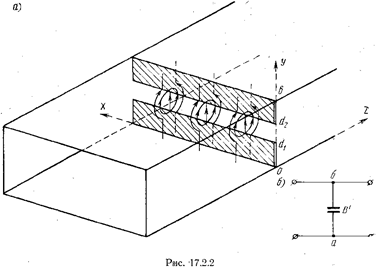
Аналогичным образом выполняется электродинамический анализ диафрагмы, изображенной на рис. 17.2.2а. Нормированная проводимость 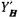 описывается ф-лой (17.2.37), где  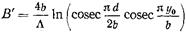(17.2.39) и ; .

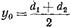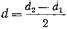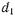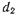При любых значениях и проводимость В' в (17.2.39) положительна, т. е. введение диафрагмы, изображенной на рис. 17.2.2а, соответствует включению в эквивалентную длинную линию параллельного емкостного сопротивления, как показано на рис. 17.2.26. Поэтому рассматриваемая диафрагма получила название емкостной.

Емкостный характер проводимости объясняется следующим образам. Между верхней и нижней половинками диафрагмы, а также вблизи нее образуются искривленные в продольной плоскости силовые линии электрического поля (см. рис. 17.2.2а). Поэтому реактивное поле вблизи диафрагмы состоит преимущественно из нераспространяющихся волн Е. Используя равенства (14.1.13) и (14.1.14), можно показать, что у нераспространяющихся волн Е 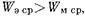 что и обусловливает емкостный характер проводимости диафрагмы.

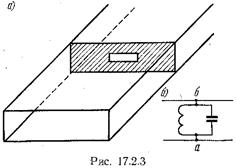
Диафрагма на рис. 17.2.3а образована совмещенными в одной плоскости двумя диафрагмами: индуктивной и емкостной. Поэтому эквивалентная схема этой диафрагмы имеет вид параллельного контура (рис. 17.2.36). Диафрагма называется резонансной, так как на той частоте, где 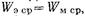 реактивная проводимость диафрагмы для волны  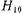равна нулю. Падающая волна без отражений проходит сквозь диафрагму. Проводимость диафрагмы, как у обычного параллельного контура, на частотах, выше резонансной, имеет емкостный характер, а на частотах ниже резонансной - индуктивный характер.

 

 

17.3. Реактивный стержень в прямоугольном волноводе

 

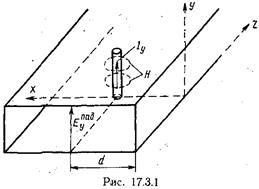
Реактивным стержнем называется металлический проводник, введенный в волновод. Рассмотрим тонкий стержень в прямоугольном волноводе, ось которого параллельна узкой стенке волновода (рис. 17.3.1 и 17.3.2). Эквивалентная схема тонкого реактивного стержня (штыря), как и в случае диафрагмы, - чисто реактивное сопротивление, включенное в линию параллельно.

Даже приближенный электродинамический анализ штыря неполной высоты 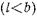 весьма труден из-за сложности поля вблизи штыря. Поэтому ограничимся рассмотрением стержня, равного по высоте размеру узкой стенки волновода (рис. 17.3.1). В этом случае введение штыря не нарушает регулярности волновода вдоль оси Y, и ближнее поле, как и в случае индуктивной диафрагмы, полностью описывается волнами типа  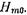Для упрощения анализа предположим, что штырь выполнен из идеально проводящего металла, его радиус много меньше длины волны 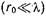, линейного размера широкой стенки волновода  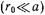и расстояния до любой из боковых узких стенок волновода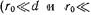

Полное поле в волноводе, образовавшееся в результате дифракции волны 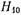на штыре, является суперпозицией двух полей: первичного падающего (волна 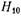) и вторичного, получающегося в результате действия токов, наведенных на штырь. Так как силовые линии магнитного поля волны  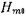перпендикулярны оси штыря, то ток проводимости ориентирован параллельно оси штыря (рис. 17.3.1). Ввиду малости диаметра штыря можно пренебречь изменением амплитуд и фаз магнитного поля по периметру штыря и считать, что тони проводимости по всей поверхности имеют одинаковые амплитуду и фазу.

Обозначим полный ток, текущий по штырю, через 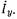 Так как диаметр штыря весьма мал, то можно для упрощения анализа ввести понятие об эквивалентной объемной плотности тока  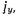полагая ее одинаковой во всех точках поперечного сечения, т. е. равной  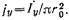Реально ток из-за явления скин-эффект а течет по тонкому поверхностному слою. В пределе при  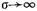толщина этого слоя стремится к нулю.

Вне штыря ток равен нулю, поэтому 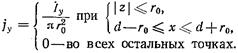 (17.3.1)

Ток проводимости 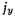 является единственным источником вторичного поля. Для нахождения этого поля воспользуемся ур-нием (5.1.10), которое в рассматриваемом 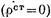случае принимает вид  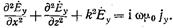(17.3.2)

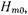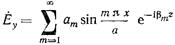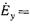
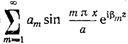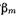Вторичное поле, как указывалось выше, является суперпозицией бесконечного числа волн  разбегающихся от штыря. Поэтому при z>0 , а при z<0  , где  - коэффициент распространения волны  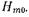Эти равенства удобно записать в виде одного выражения

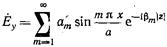 (17.3.3)

Подставляя (17,3.3) в (17.3.2), получаем 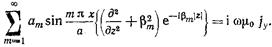 (17.3.4)

Умножая обе части соотношения (17.3.4) на 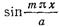 и интегрируя по координате х от 0 до а, а по координате z от  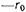до 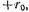 приходим к равенству

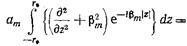
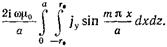 (17.3.5)

Разбивая интеграл в левой части (17.3.5) на два: 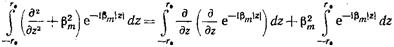 (17.3.6)

и вычисляя первый из них, получаем 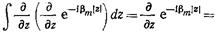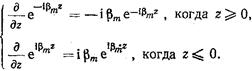(17.3.7)

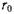
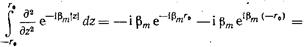
Отсюда при малом  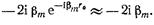(17.3.8)

Аналогично для второго интеграла 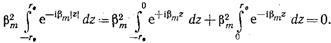 (17.3.9)

Следовательно, 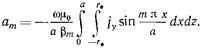 (I7.3.I0)

Согласно (17.3.1) плотность тока проводимости - величина постоянная, и ее можно вынести из-под знака интеграла в (17.3.10): 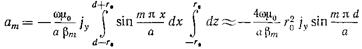 . (17.3.11)

При записи (17.3.11) было использовано справедливое при малых 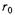 равенство  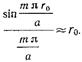Подставляя (17,3.11) в (17.3,3), получаем  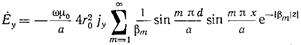. (17.3.12)

Так как волновод является предельным для всех волн, начиная с 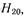 то при  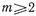согласно (17.2.18) 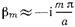. Поэтому ряд (17.3.12) можно записать в виде

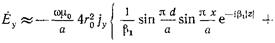
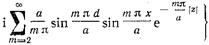. (17.3.13).

Если почленно продифференцировать бесконечный ряд в (17.3.13) по d

 (17.3.14)

и заменить входящие в (17.3.14) синус и косинус по (формуле Эйлера, то каждая из получившихся четырех бесконечных сумм оказывается сходящейся геометрической прогрессией со знаменателем 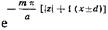. Выполнив суммирование по известной формуле для геометрической прогрессии, приходим к равенству

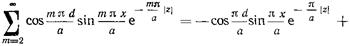
 (17.3.15)

Интегрируя обе части равенства (17.3.15) по d, находим сумму ряда в (17.3.13):

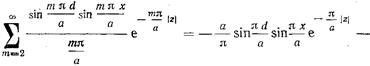
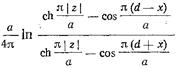, (17.3.16).

что позволяет с учетом (17.3.1) записать (17.3.3) в виде

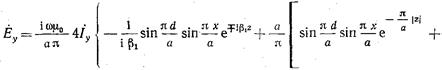
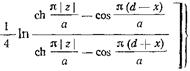• (17.3.17>

Первое слагаемое в фигурных скобках соотношения (17.3.17) соответствует двум бегущим то волноводу в обе стороны от штыря волнам 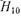: одной, распространяющейся в том же направлении, что и падающая 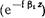, и второй (отраженной), распространяющейся в направлении, противоположном направлению распространения падающей волны 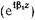. Слагаемое в квадратных скобках описывает структуру 'ближнего реактивного по характеру поля по обеим сторонам от штыря. Действительно, пр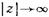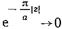и  и 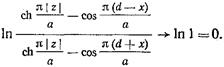 (17.3.18)

Эти соотношения, как нетрудно проверить, хорошо выполняются уже при 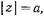 т. е. на расстоянии от штыря, равном размеру широкой стенки, структура поля в волноводе практически не отличается от структуры поля волны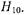

Напряженность электрического поля падающей на штырь волны 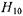 единичной амплитуды согласно (14.1.26) записывается в виде  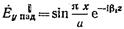(17.3.19)

Так как штырь предполагается выполненным из идеального проводника, то на его поверхности касательная составляющая электрического поля равна нулю. Как отмечалось выше, полное поле в волноводе является суперпозицией падающего и вторичного полей. Поэтому на поверхности штыря (при 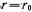)  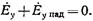(17.3.20)

При анализе мы пренебрегли изменением полей на поверхности штыря. Поэтому равенство (17.3.20) можно применить к какой-либо одной точке, лежащей на поверхности штыря. Полагая, например, z=0 и 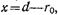 получаем

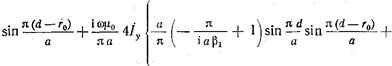
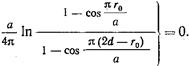 (17.3.21)

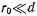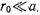Так как  и  то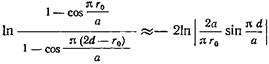

и поэтому 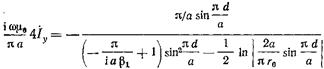 . (17.3.22)

Амплитуда отраженной волны согласно (17.3.1), (17.3.11) и (17.3.22) равна

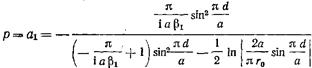 . (17.3.23)

Нормированная проводимость в сечении z=0, где включен штырь,, определяется по ф-ле (16.3.10) и равна 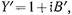 где 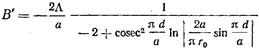 (17.3.24)

Так как при 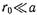 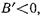то введение в волновод штыря, у которого  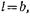соответствует параллельному включению в эквивалентную длинную линию индуктивности. Поэтому рассматриваемый штырь называют индуктивным. Индуктивный характер вносимого сопротивления объясняется, как и в случае индуктивной диафрагмы, тем, что реактивное поле вблизи штыря образуется волнами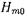 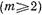, у которых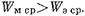

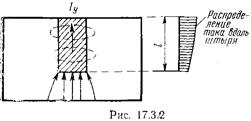
Когда высота штыря меньше расстояния между широкими стенками волновода (рис. 17.3.2), то картина несколько меняется. При этом штырь можно рассматривать как отрезок однопровод-ной линии передачи (гл. 14). В зазоре между торцом штыря и нижней стенкой волновода образуется повышенная концентрация энергии электрического поля, т. е. штырь нагружен на торцевую емкость. Так как штырь предполагается весьма тонким, то эта - емкость невелика. Поэтому распределение тока вдоль штыря близко к синусоидальному, как в линии, работающей в режиме холостого хода (рис. 17,3.2). Из теории длинных линий известно, что разомкнутый на конце отрезок линии при длине, меньшей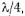

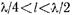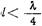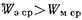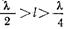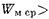
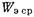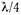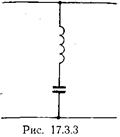
имеет емкостное, а при длине  - индуктивное входное сопротивление. Следовательно, при  в ближнем поле штыря  и введение штыря эквивалентно включению в линию параллельной емкости. При- в ближнем поле и введение штыря такой длины соответствует включению в линию параллельной индуктивности. При длине штыря, равной , наступает резонанс, т. е. 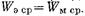 Подобная зависимость входного сопротивления от частоты характерна, как известно, для последовательного контура. Поэтому полная эквивалентная схема тонкого штыря неполной высоты имеет вид последовательного контура, включенного параллельно в линию (рис 17.3.3). При резонансе  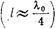входное сопротивление контура равно нулю, волновод оказывается замкнутым накоротко, и вся энергия падающей волны полностью отражается от штыря.

На практике ввиду конечной проводимости металла, из которого выполняется штырь, модуль коэффициента отражения несколько меньше единицы, а коэффициент прохождения отличен от нуля.

При очень малом зазоре между торцом штыря и нижней стенкой волновода торцевая емкость весьма велика. В результате распределение тока вдоль штыря приближается к равномерному. Параметры такого штыря мало отличаются от параметров штыря, введенного на полную высоту волновода.

//л6-1 ВП ПрУСВЧ