2014-02-13
1493
Кольца
Кольцом называется (непустое) множество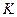 
, на котором определены две операции (сложение + и умножение ´), обладающие следующими свойствами:
1.Множество 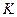относительно операции сложения образует коммутативную группу с нейтральным элементом 0.
2.Операция умножения ассоциативна: для любых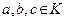 
.
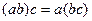3.В множестве K существует мультипликативная единица e ¹ 0, т.ч. a ´ e = e ´ a.
4.Операции сложения и умножения подчиняются дистрибутивному закону:
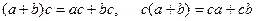для любых 
.
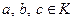При этом множество 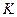, рассматриваемое лишь относительно операции сложения, называется аддитивной группой кольца.
Примеры колец.
Множество целых чисел с операциями сложения и умножения – кольцо целых чисел Z
1. Множество многочленов от одного неизвестного с действительными коэффициентами с операциями сложения и умножения многочленов – кольцо многочленов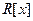 
.
2. Множество классов вычетов – кольцо классов вычетов Z n.
Поскольку операции над классами вычетов сводятся к операциям над числами из этих классов, то свойства ассоциативности и коммутативности этих операций вытекают из аналогичных свойств числового сложения и умножения. То же замечание относится и к свойству дистрибутивности. Роль нулевого элемента при сложении играет класс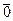 
. Противоположным элементом для класса вычетов 
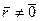является класс 
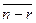. Из определения сложения классов следует, что 
.
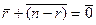Кольцо называется коммутативным, если для любых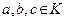 
.
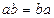В примерах 1-3 все кольца коммутативные.
Определение. Элемент кольца a Î K называется обратимым, если существует элемент b Î K, т.ч. a b = 1.
В кольце целых чисел Z обратимы лишь 1 и –1, всякое другое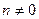 
в кольце Z не имеет обратного, так как 
.
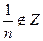Утверждение. Множество обратимых элементов кольца образует мультипликативную группу.
Пример. Z n* – группа обратимых элементов кольца Z n.
