Finish
Gо to 1
Gо to 1
шагmD
20 хi = хi + 1
yi = yi + 1
i = i+ 2хi - 2уi+ 2
Переменная предела устанавливается в нуль для окончания работы алгоритма на горизонтальной оси, в результате генерируется окружность в первом квадранте. Если необходим лишь один из октантов, то второй октант можно получить с помощью установки Предел = Integer (R/sqrt(2)), а первый - с помощью отражения второго октанта относительно прямой у = х (рис. 5.1). Блок-схема алгоритма приводится на рис. 5.5.
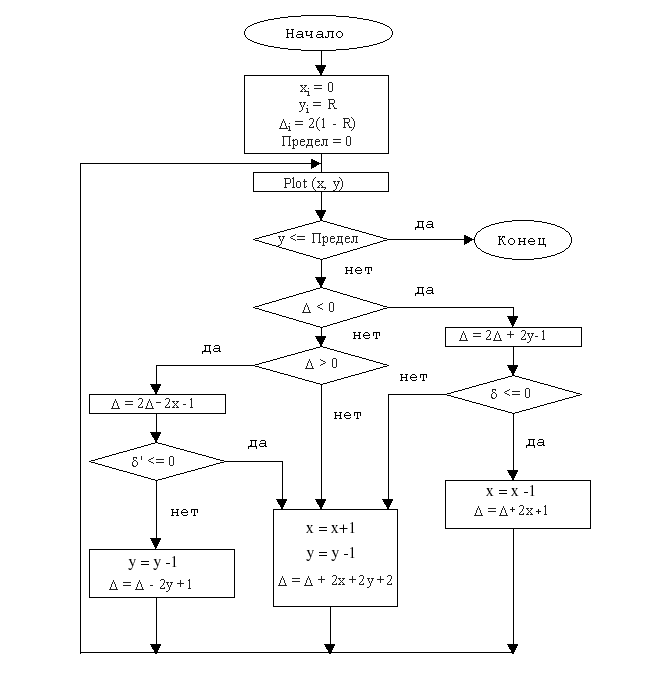 |
Рис. 5.5. Блок-схема пошагового алгоритма Брезенхема для генерации окружности в первом квадранте.
Пример 5.1. Алгоритм Брезенхема для окружностию
Рассмотрим окружность радиусом 8 с центром в начале координат. Генерируется только первый квадраннт.
начальные установки
x = 0
y = 8
= 2(1-8) = -14
Предел = 0
Пошаговое выполнение основного цикла
1 Plot (0,8)
yi > Предел (продолжать)
i < 0 go to 2
2 go to 10
10 x = 0+1 = 1
i = -14 +2 + 1 = -11
go to 1
1 Plot (1,8)
yi > Предел (продолжать)
i < 0 go to 2
2 go to 10
10 x = 1+1 = 1
i = -11 +2(2) + 1 = -6
go to 1
1 Plot (2,8)
...
Продолжать
Результаты всех последовательных проходов алгоритма сведены в таблицу. Список пикселов выбранных алгоритмов состоит из (0,8), (1,8), (2,8), (3,7), (4,7), (5,6), (6,5), (7,4), (7,3), (8,2), (8,1), (8,0).
| Plot | i | | ' | x | y |
| -14 | |||||
| (0,8) | |||||
| -11 | -13 | ||||
| (1,8) | |||||
| -6 | -7 | ||||
| (2,8) | |||||
| -12 | |||||
| (3,7) | |||||
| -3 | |||||
| (4,7) | |||||
| -3 | |||||
| (5,6) | |||||
| (6,5) | |||||
| -11 | |||||
| (7,4) | |||||
| (7,3) | |||||
| -7 | |||||
| (8,2) | |||||
| (8,1) | |||||
| (8,0) |
алгоритм завершен.
Результаты показаны на рис.5.6. вместе с реальной окружностью. Алгоритм легко обобщается для других квадрантов или дуг окружностей.
 |
Рис. 5.6. Результаты работы пошагового алгоритма Брезенхема генерации окружности.
Растром называется прямоугольная сетка точек, формирующих изображение на экране компьютера. Каждая точка растра характеризуется двумя параметрами: своим положением на экране и своим цветом, если монитор цветной, или степенью яркости, если монитор черно-белый. Поскольку растровые изображения состоят из множества дискретных точек, то для работы с ними необходимы специальные алгоритмы. Рисование отрезка прямой линии - одна из простейших задач растровой графики. Смысл ее заключается в вычислении координат пикселов, находящихся вблизи непрерывных отрезков, лежащих на двумерной растровой сетке.
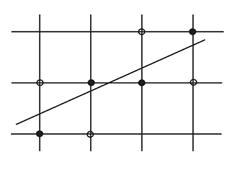
Рис. 28. Растеризация отрезка прямой линии.
Термин “пиксел” образован от английского pixel (picture element - элемент изображения) - то есть точка на экране. Будем считать, что пикселы имеют целочисленные координаты. На первый взгляд кажется, что эта задача имеет простое решение. Пусть конечные точки отрезка имеют целочисленные координаты, и уравнение прямой, содержащей отрезок: 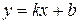 . Не нарушая общности, будем также считать, что тангенс угла наклона прямой лежит в пределах от 0 до 1. Тогда для изображения отрезка на растре достаточно для всех целых
. Не нарушая общности, будем также считать, что тангенс угла наклона прямой лежит в пределах от 0 до 1. Тогда для изображения отрезка на растре достаточно для всех целых 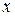 , принадлежащих отрезку, выводить на экран точки с координатами
, принадлежащих отрезку, выводить на экран точки с координатами 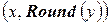 . Однако в этом методе присутствует операция умножения
. Однако в этом методе присутствует операция умножения 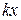 . Хотелось бы иметь алгоритм без частого использования операции умножения вещественных чисел. Избавиться от операции умножения можно следующим образом. Поскольку
. Хотелось бы иметь алгоритм без частого использования операции умножения вещественных чисел. Избавиться от операции умножения можно следующим образом. Поскольку 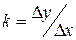 , то один шаг по целочисленной сетке на оси
, то один шаг по целочисленной сетке на оси 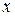 будет соответствовать
будет соответствовать 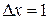 . Отсюда получаем, что
. Отсюда получаем, что 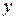 будет увеличиваться на величину
будет увеличиваться на величину 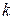 . Итерационная последовательность выглядит следующим образом:
. Итерационная последовательность выглядит следующим образом:
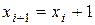 ,
, 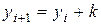
Когда 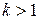 , то шаг по
, то шаг по 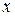 будет приводить к шагу по
будет приводить к шагу по 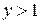 , поэтому
, поэтому 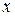 и
и 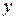 следует поменять ролями, придавая
следует поменять ролями, придавая 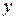 единичное приращение, а
единичное приращение, а 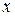 будет увеличиваться на
будет увеличиваться на 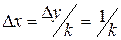 единиц. Этот алгоритм все же не свободен от операций с вещественными числами. Наиболее изящное решение задачи растровой развертки отрезков прямых было найдено Брезенхемом. В его алгоритме вообще не используются операции с вещественными числами, в том числе операции умножения и деления.
единиц. Этот алгоритм все же не свободен от операций с вещественными числами. Наиболее изящное решение задачи растровой развертки отрезков прямых было найдено Брезенхемом. В его алгоритме вообще не используются операции с вещественными числами, в том числе операции умножения и деления.
Для вывода формул алгоритма Брезенхема рассмотрим рис. 29.
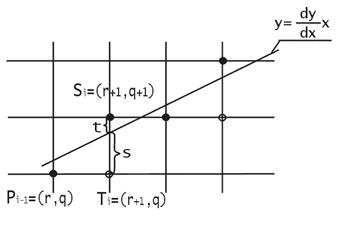
Рис. 29. Рисование отрезков прямых по методу Брезенхема.
Пусть начало отрезка имеет координаты 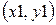 , а конец
, а конец 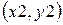 . Обозначим
. Обозначим 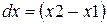 ,
, 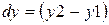 . Не нарушая общности, будем считать, что начало отрезка совпадает с началом координат, и прямая имеет вид
. Не нарушая общности, будем считать, что начало отрезка совпадает с началом координат, и прямая имеет вид 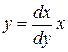 , где
, где 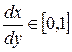 . Считаем что начальная точка находится слева. Пусть на
. Считаем что начальная точка находится слева. Пусть на 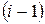 -м шаге текущей точкой отрезка является
-м шаге текущей точкой отрезка является 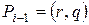 . Выбор следующей точки
. Выбор следующей точки 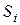 или
или 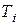 зависит от знака разности
зависит от знака разности 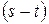 . Если
. Если 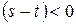 , то
, то 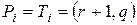 и тогда
и тогда 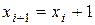 ,
, 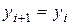 , если же
, если же 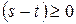 , то
, то 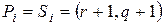 и тогда
и тогда 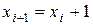 ,
, 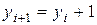 .
.
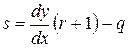 ,
, 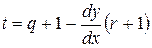 ,
,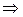
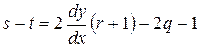
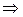
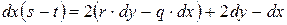 .
.
Поскольку знак 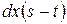 совпадает со знаком разности
совпадает со знаком разности 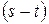 , то будем проверять знак выражения
, то будем проверять знак выражения 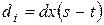 . Так как
. Так как 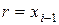 и
и 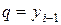 , то
, то 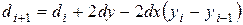 .
.
Пусть на предыдущем шаге 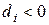 , тогда
, тогда 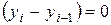 и
и 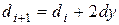 . Если же на предыдущем шаге
. Если же на предыдущем шаге 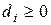 , то
, то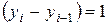 и
и 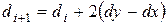 .
.
Осталось узнать как вычислить 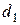 . Так как при
. Так как при  :
:
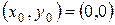 ,
,  .
.
Далее приводится листинг процедуры на языке Паскаль, реализующей алгоритм Брезенхема.
Procedure Bresenham(x1,y1,x2,y2,Color: integer);
var
dx,dy,incr1,incr2,d,x,y,xend: integer;
begin
dx:= ABS(x2-x1);
dy:= Abs(y2-y1);
d:=2*dy-dx; {начальное значение для d}
incr1:=2*dy; {приращение для d<0}
incr2:=2*(dy-dx); {приращение для d>=0}
if x1>x2 then {начинаем с точки с меньшим знач. x}
begin
x:=x2;
y:=y2;
xend:=x1;
end
else
begin
x:=x1;
y:=y1;
xend:=x2;
end;
PutPixel(x,y,Color); {первая точка отрезка}
While x<xend do
begin
x:=x+1;
if d<0 then
d:=d+incr1 {выбираем нижнюю точку}
else
begin
y:=y+1;
d:=d+incr2; {выбираем верхнюю точку, y-возрастает}
end;
PutPixel(x,y,Color);
end;{while}
end;{procedure}
Перед тем, как исследовать методы получения изображений более сложных, чем отрезки прямых, рассмотрим проблему, незримо присутствующую в большинстве задач компьютерной графики. Эта проблема отсечения изображения по некоторой границе, например, по границе экрана, или, в общем случае, некоторого прямоугольного окна. Рассмотрим эту задачу применительно к отрезкам прямых. Некоторые из них полностью лежат внутри области экрана, другие целиком вне ее, а некоторые пересекают границу экрана. Правильное отображение отрезков означает нахождение точек пересечения их с границей экрана и рисование только тех их частей, которые попадают на экран. Один из очевидных способов отсечения отрезков состоит в определении точек пересечения прямой, содержащей отрезок, с каждой из четырех прямых, на которых лежат границы окна и проверки не лежит ли хотя бы одна точка пересечения на границе. В этом случае для каждой пары сторона-отрезок необходимо решать систему из двух уравнений, используя операции умножения и деления. При этом удобно параметрическое задание прямых:
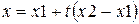
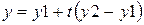 .
.
Для 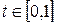 эти уравнения определяют точки, находящиеся между
эти уравнения определяют точки, находящиеся между 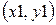 и
и 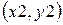 . Специальной проверки требует случай, когда отрезок параллелен стороне окна. Пусть координата x точки пересечения найдена, тогда
. Специальной проверки требует случай, когда отрезок параллелен стороне окна. Пусть координата x точки пересечения найдена, тогда
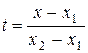
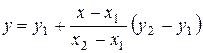
 2014-02-09
2014-02-09 2362
2362







