2014-02-13
635
Алгоритм построения минимального каркаса
Пусть G (X, E) - связный нагруженный граф с p вершинами.
Шаг 1°. В качестве первого ребра искомого минимального каркаса выбираем ребро e 1 с наименьшим весом m(e 1). Если таких ребер несколько, то берем любое из них.
Шаг 2°. В качестве второго ребра берем ребро e 2 из множества E\ { e 1}, имеющее наименьший вес m(e 2), и такое, что множество { e 1, e 2} не содержит простых циклов. Если таких ребер несколько, то берем любое из них.
Шаг 3°. В качестве третьего ребра выбираем такое ребро e 3 из множества E\ { e 1, e 2}, которое имеет наименьший вес m(e 2) и для которого множество { e 1, e 2, e 3} не содержит простых циклов. Если таких ребер несколько, берем любое из них.
Указанный процесс повторяется и через некоторое число k шагов дает множество E = { e 1, e 2, …, ek }, к которому нельзя добавить ребро без появления цикла. Подграф G 1(X, E 1) и является минимальным каркасом графа G (X, E).
В силу свойства 6° из теоремы 6.1 построенный подграф G 1(X, E 1) является деревом, поэтому k = p –1. Доказательство минимальности каркаса G 1(X, E 1) разобьем на два этапа. Пусть сначала G (X, E) – полный граф, у которого веса всех ребер различны, и пусть G 2(X, E 2) – минимальный каркас графа G. Если E 2 ¹ E 1, то рассмотрим el – первое из ребер множества E 1, не принадлежащее E 2. В графе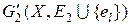 
в силу свойства 6° теоремы 6.1 существует единственный простой цикл m. Цикл m содержит ребро e 0Ï E 1. Граф G 3(X, E 3), где 
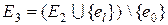, не содержит циклов и имеет n – 1 ребро, поэтому он является деревом. Множество { e 1, e 2, …, el -1, e 0} содержится в E 2 и поэтому не содержит циклов. Тогда в силу рассмотренного выше алгоритма m(e 0) > m(e l). Отсюда следует, что суммарный вес дерева G 3(X, E 3) меньше веса дерева G 2(X, E 2). Это противоречит минимальности каркаса G 2, поэтому E 2 = E 1 и G 1(X, E 1) – единственный минимальный каркас графа G.
|
|
|
Пусть теперь G (X, E) – произвольный нагруженный связный граф. Если m(e 1) = m(e 2), то сделаем замену
m(e 1) ® m'(e 1) = m(e 1) + e,
m(e 2) ® m'(e 2) = m(e 2) + 2e,
взяв такое e, чтобы сохранились соотношения весов m(e 1) и m(e 2) с другими весами. Сделаем граф G полным, добавив такие ребра di, что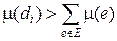 
. В полученном графе единственным минимальным каркасом будет каркас, полученный с помощью рассмотренного алгоритма. Легко видеть, что этот каркас будет минимальным и в исходном графе G (X, E).
На рис. 6.4 изображены нагруженный граф G и его минимальный каркас G 1.
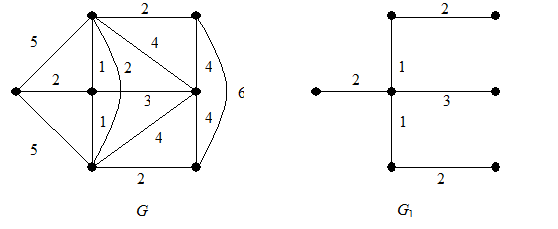
Рис. 6.4
