Пересечение графов

Пусть G₁(X₁,E₁) и G₂(X₂,E₂) – произвольные графы. Пересечением G₁ÇG₂ графов G₁ и G₂ называется граф с множеством вершин X₁ÇX₂ с множеством ребер (дуг) E = E₁ÇE₂

Операция пересечения обладает следующими свойствами, которые следуют из определения операции и свойств операций на множествах:

G₁ÇG₂ = G₂ÇG₁ – свойство коммутативности;

G₁Ç (G2ÇG3) = (G1ÇG2) Ç G₃ – свойство ассоциативности.

Для того чтобы операция пересечения была всеобъемлющей, необходимо ввести понятие пустого графа. Граф G(X,E) называется пустым, если множество X вершин графа является пустым (X=Æ). Заметим, что в этом случае и множество E ребер (дуг) графа также пустое множество (E=Æ). Пустой граф обозначается символом Æ. Такой граф может быть получен в результате выполнения операции пересечения графов, у которых X₁ÇX₂=Æ. В этом случае говорят о непересекающихся графах.

Рассмотрим выполнение операции пересечения графов, изображенных на рис. 4.2. Для нахождения множества вершин результирующего графа запишем множества вершин исходных графов и выполним над этими множествами операцию пересечения:

X₁ = {x₁, x₂, x₃}; X₂ = {x₁, x₂, x₃, x₄};

X = X₁ÇX₂ = {x₁, x₂, x₃}.

Аналогично определяем множество E дуг результирующего графа:

E₁ = {(x₁, x₂), (x₁, x₃), (x₂, x₁), (x₂, x₃), (x₃, x₂)};

E₂ = {(x₁, x₃), (x₂, x₁), (x₂, x₃), (x₂, x₄), (x₃, x₁)};

E = E₁ÇE₂ = {(x₁, x₃), (x₂, x₁)}.

Графы G₁(X₁,E₁), G₂(X₂,E₂) и их пересечение приведены на рис 4.2.

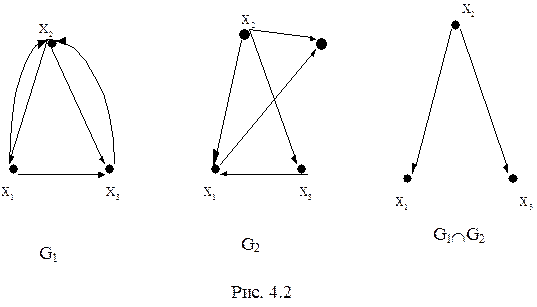
Операция пересечения графов может быть выполнена в матричной форме.

Теорема 4.2. Пусть G₁ и G₂ – два графа (ориентированные или неориентированные одновременно) с одним и тем же множеством вершин X, и пусть A₁ и A₂ – матрицы смежности вершин этих графов. Тогда матрицей смежности вершин графа G1ÇG2 является матрица A = A₁ÇA₂ образованная поэлементным логически умножением матриц A₁ и A₂.

Рассмотрим выполнение операции пересечения для графов с несовпадающим множеством вершин.

Пусть G₁(X₁,E₁) и G₂(X₂,E₂) – графы без параллельных ребер, множества X₁ и X₂ вершин графов не совпадают, а A₁ и A₂ – матрицы смежности вершин графов. Для таких графов операция пересечения может быть выполнена так.

В соответствии с определением операции пересечения графов найдем множество вершин результирующего графа как X₁ÇX₂. Построим вспомогательные графы G’₁ и G’₂, множества вершин которых есть множество X₁ÇX₂, а множество ребер (дуг) определяется множествами E’₁ и E’₂ всех ребер (дуг), инцидентных этим вершинам. Очевидно, что матрицы A’₁ и A’₂ смежности вершин этих графов могут быть получены из матриц A₁ и A₂ путем удаления из них столбцов и строк, соответствующих вершинам, не вошедшим во множество X1ÇX2.

Применив к графам G’₁ и G’₂ теорему 4.2, найдем матрицу смежности вершин графа G’₁ÇG’₂ как A’₁ÇA’₂. Очевидно, что полученной матрице смежности вершин соответствует граф, множество вершин которого равно X₁ÇX₂, а множество ребер определяется, как E₁ÇE₂, что соответствует операции пересечения графов.

Пример 4.2. Выполнить в матричной форме операцию пересечения графов G₁ и G₂, представленных на рис. 4.2.

Составим матрицы смежности вершин исходных графов.

x1

x2

x3

x1

x2

x3

x4

x1

x1

A1

=

x2

A2

=

x2

x3

x3

x4

Находим множество вершин X результирующего графа.

X = X₁ÇX₂ = {x₁, x₂, x₃}.

Составим матрицы смежности вершин вспомогательных графов G’₁ и G’₂.

			x1	x2	x3				x1	x2	x3
		x1						x1
A’1	=	x2				A’2	=	x2
		x3						x3

Найдем матрицу смежности вершин A = A₁ Ç A₂

			x1	x2	x3
		x1
A’1ÇA’2	=	x2
		x3

Полученная матрица смежности вершин A’₁ Ç A’₂ соответствует графу G₁ÇG₂, изображенному на рис.4.2.