Способы детальной разбивки закруглений.
Для строительства подъездных дорого на промплощадок кроме главных точек закруглений (НК, СК, КК) необходимо на местности получить ряд дополнительных точек на кривой. Т.е. выполнить детальную разбивку.
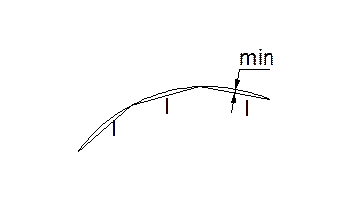 Дополнительные точки на кривой закрепляют через равные промежутки е из соображений, чтобы стрелка прогиба дуги должна быть настолько мала, чтобы вписанный многоугольник можно было практически принять за дугу окружности.
Дополнительные точки на кривой закрепляют через равные промежутки е из соображений, чтобы стрелка прогиба дуги должна быть настолько мала, чтобы вписанный многоугольник можно было практически принять за дугу окружности.
Выбор величины хорды l зависит от радиуса кривой R и назначения кривой.
Рекомендуемые значения интервала разбивки.
| R | l | |
| больше 500 м | 20 м | |
| от 100 до 500 м | 10 м | |
| до 100 м | 5 м |
Способы детальной разбивки:
· способ прямоугольных координат;
· полярный (способ углов);
· продолжением хорд.
Способ прямоугольных координат:
1. Положение точек на кривой через равные промежутки l определяется прямоугольными координатами (x, y)
2. 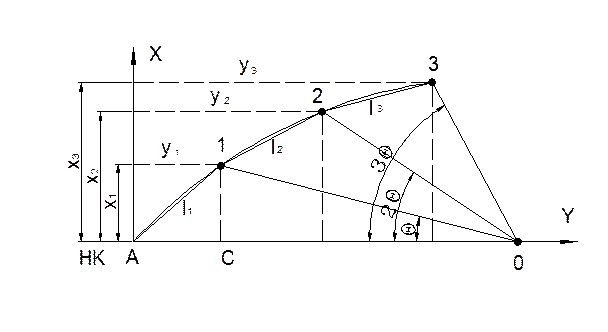 Начало координат – НК или КК.
Начало координат – НК или КК.
Ось абсцисс – линия тангенса (касательная)
3. Для вычисления координат x,y точек детальной разбивки предварительно вычисляют центральный угол для дуги l.
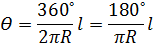
4. Далее решая прямоугольный треугольник ОС1 получим
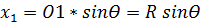
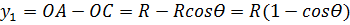
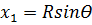
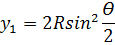
5. Аналогичным образом вычисляют координаты последующих точек:
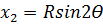
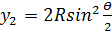
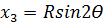
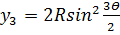
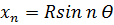
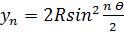
6. Определение положения точек 1,2,3 кривой на местности сводится к откладыванию рулеткой от НК (КК) отрезков X 1, X 2, X 3… y 1, y 2, y 3
7. Разбивку ведут от НК до СК, а затем от КК до С.
8. Достоинство способа:
- положение каждой точки определяется независимо;
- при переходе от одной точки к другой погрешность не накапливается.
9. Способ применяется в открытой равнинной местности.
Полярный способ (способ углов)
1. 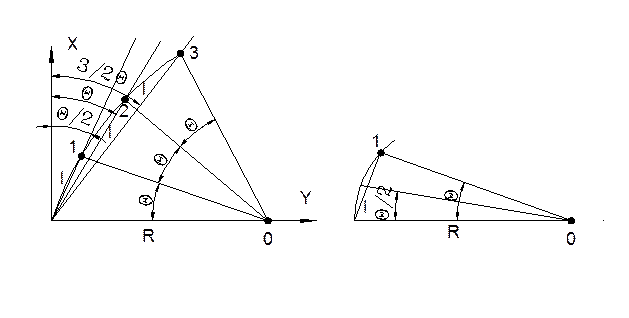 Способ базируется на положении геометрии о том, что угол с вершиной в какой – либо точке кривой образованный касательной и секущей, равен половине соответствующего центрального угла.
Способ базируется на положении геометрии о том, что угол с вершиной в какой – либо точке кривой образованный касательной и секущей, равен половине соответствующего центрального угла.
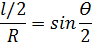
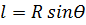
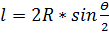 , откуда:
, откуда: 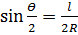
2. Положение точек на местности определяется линейно-угловыми засечками:
- теодолит устанавливается в НК (или КК)
- от направления тангенса (касательная) откладывают последовательно углы: 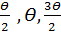 и т.д.
и т.д.
- отложив рулеткой по направлению первого визирного луча отрезок l и закрывают на местности точку 1.
- из точки 1 протягивают рулетку до пересечения отрезком l со вторым визирным лучом и закрепляют точку 2 и т.д.
3. Недостаток способа:
- снижение точности детальной разбивки с увеличением числа точек.
4. Способ применяется на косогорах, насыпях и в полузакрытых равниной местности.
 2014-02-09
2014-02-09 2041
2041








