Пример 1. Даны две простые дроби. Составить алгоритм получения дроби, являющейся результатом их деления.
Решение. В алгебраической форме решение задачи выглядит следующим образом:
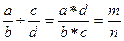 .
.
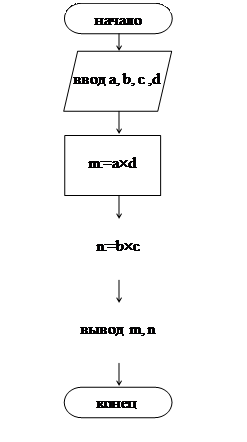
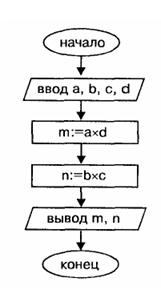
Исходными данными являются четыре целые величины: а, b, с, d. Результат - два целых числа m и n.
 | |||
| |||
 | |||
 |
Тест: a = 3, b=4, c=5, d=6.
Результат: m = 18, n = 20.
Пример 2. Даны две переменные величины X и Y. Требуется произвести между ними обмен значениями. Обмен происходит через промежуточную переменную Z.
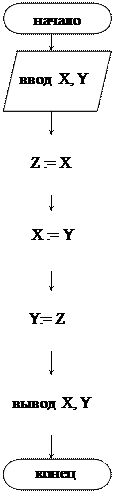
 ввод X,Y
ввод X,Y
Z:=X
X:=Y
 Y:=Z
Y:=Z
вывод X, Y

Тест: x = 3, y = -7.
 Результат: x = -7, y = 3.
Результат: x = -7, y = 3.
 |
Пример 3. Даны три вещественных числа А, В, С. Найти наибольшее среди них.
Решение.1 способ.
Сначала определяется большее среди двух значений А и В, затем большее между найденным значением и величиной С. Алгоритм имеет структуру двух последовательных ветвлений.
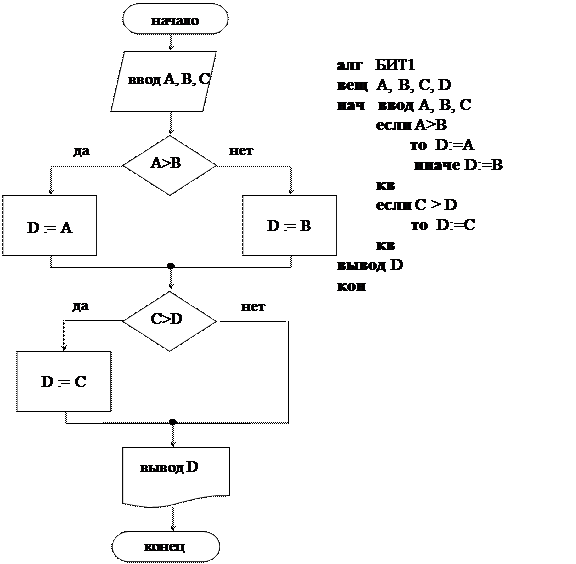
Тест: a = 3, b = 6, c = 2.
Результат: D = 6.
2 способ. Задача решена с помощью вложенных ветвлений.
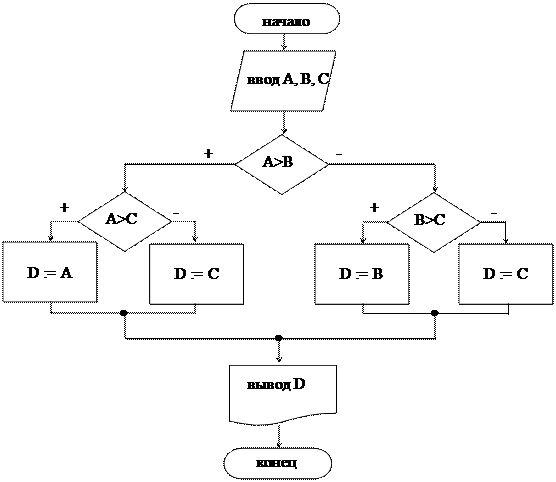
Пример 4. Дано целое положительное число N. Вычислить факториал этого числа: N! = 1 * 2 * 3 *... * N
Решение. Задача решается c помощью циклического алгоритма. Составим два варианта алгоритма: цикла с параметром и с применением цикла с предусловием.
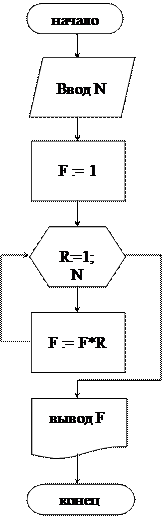 | |||
| |||
Тест: N = 5.
Результат: факториал F = 120.
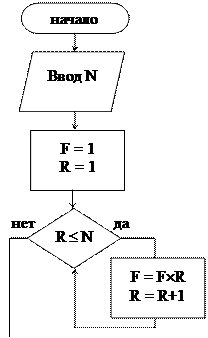 | |||
| |||


 |
 2014-02-09
2014-02-09 912
912







