2014-02-09
551
Линейная зависимость векторов
Лекция 2
Задания для самостоятельной работы
1. Начертите произвольный вектор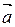 
. Постройте векторы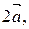 
.
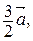
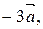
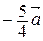2. Даны векторы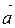 
и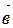 
. Постройте векторы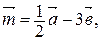 
.
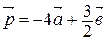3. Упростите выражение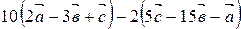 
.
4. Будут ли векторы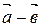 
и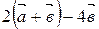 
коллинеарны и почему, если 
?
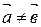5. Будут ли векторы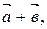 
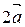и 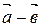компланарны и почему?
Линейной комбинацией векторов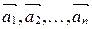 
называется вектор 
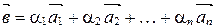, где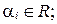 
.
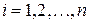Примеры линейных комбинаций:
1. Вектор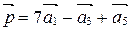 
есть линейная комбинация векторов 
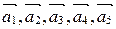(здесь 
).
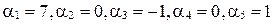2. Вектор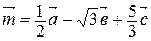 
есть линейная комбинация векторов 
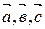(здесь 
).
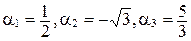Система векторов 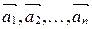называется линейно зависимой, если существуют такие действительные числа 
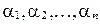, не все равные 0 одновременно, что выполняется векторное равенство:
.
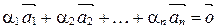Если равенство 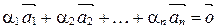выполняется только при 
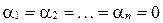, то система векторов 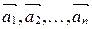называется линейно независимой.
