Основные определения. Класс линейных функций

Задача минимизации ДНФ

Класс линейных функций

Класс монотонных функций

Класс самодвойственных функций

Класс функций, сохраняющих единицу

Класс функций, сохраняющих ноль

Функция f(х₁,..., х_n) называется сохраняющей ноль,если она на нулевом наборе принимает значение 0, то есть f(0,..., 0) = 0.

Пример. f(х) = 0, f(х) = х, f(х₁, х₂) = х₁ • х₂, f(х₁, х₂) =
х₁ Ú х₂ сохраняют ноль; f(х) = 1, f(х) =`х, f(х₁, х₂) = х₁ ® х₂ не сохраняют ноль.

Лемма 1. Из функций, сохраняющих ноль, супер­позицией можно получить только функции, сохраняющие ноль.

Доказательство. Функции, равные переменным, сох­ра­няют ноль. Поэтому достаточно показать, что функция

Ф(х₁,..., х_n) = f(f₁(х₁,..., х_n),..., f_m(х₁,..., х_n))

сохраняет ноль, если функции f, f_l, …, f_m сохраняют ноль. Последнее следует из

f(f₁(0,..., 0),... f_m(0,..., 0)) = f(0,..., 0) = 0.

Следствие. Полная система функций должна содер­жать хотя бы одну функцию, не сохраняющую ноль.

Функция f(х₁,..., х_n) называется сохраняющей едини­цу, если она на единичном наборе принимает значение 1, то есть f (1,..., 1) = 1.

Пример. Функции f(х) = 1, f(х) = х – сохраняют единицу; функции f(х) = 0, f(х) =`х, f(х₁, х₂) = х₁ Å х₂ – не сохраняют единицу.

Лемма 2. Из функций, сохраняющих единицу, суперпози­цией можно получить только функции, сохраняющие единицу. Доказательствоочевидно.

Следствие. Полная система функций должна содер­жать хотя бы одну функцию, не сохраняющую единицу.

Функция f (х₁,..., х_n) называется самодвойственной,если f(х₁,..., х_n) = `f(`х₁,...,`х_n).

Пример. f(х) = х, f(х) =`х – самодвойствен­ные функ­ции; f(х₁, х₂) = х₁ • х₂, f(х₁, х₂) = х₁ Ú х₂ – несамо­двой­ственные.

Лемма 3. Из самодвойственных функций суперпози­цией можно получить только самодвойственные функции.

Следствие. Полная система функций должна содер­жать хотя бы одну несамодвойственную функцию.

Набор a = (a₁,..., a_n) предшествуетнабору b = (b₁,..., b_n), если a_i £ b_i (i = l, 2,..., n). Это обозначаем как a £ b. Наборы, которые находятся в отношении £называются сравнимыми.

Функция f(х₁,..., х_n) называется монотонной,если для любой пары наборов a и b таких, что при a £ b: f(a) £ f(b).

Пример. f(х) = х, f(х₁, х₂) = х₁ • х₂, f(х₁, х₂) = х₁ Ú х₂ – монотонные функции, а f(х) =`х – немо­нотонная функция.

Лемма 5. Из монотонных функций суперпозицией мож­но получить только монотонные функции.

Следствие. Полная система функций должна содер­жать хотя бы одну немонотонную функцию.

Функция f(х₁,..., х_n) называется линейной,если полином Жегалкина этой функции имеет линейный вид:

f(х₁,..., х_n) = а₀ Å а₁ x₁ Å … Å а_n x_n,

где а_i Î {0,1} (i = 0, l,..., n).

Пример. f(х) = х, f(х) =`х = х Å 1 – линейные функции; f(х₁, х₂) = х₁ Ú х₂ = х₁ Å х₂ Å х₁•х₂ – нелинейная функция.

Лемма 7. Из линейных функций суперпозицией можно полу­чить только линейные функции.

Следствие. Полная система функций должна содержать хотя бы одну нелинейную функцию.

Таблица 2.6. Свойства функций двух переменных

Обозначе­ние функ­ции	Свойства функции
Сохра­няю­щая 0	Сохра­няю­щая 1	Самодвой­ствен­ность	Моно­тонность	Линей­ность
f1 = 0	+	–	+	+	+
f2 = х1 Ù х2	+	+	–	+	–
f3 = х1 ¬ х2	+	–	–	–	–
f4 = x1	+	+	+	+	+
f5 = х2 ¬ х1	+	–	–	–	–
f6 = x2	+	+	+	+	+
f7 = x1 Å x2	+	–	–	–	+
f8 = х 1Ú х2	+	+	–	+	–
f9 = х 1¯ х2	–	–	–	–	–
f10 = x1 ~ x2	–	+	–	–	+
f11 = `x2	–	–	+	–	+
f12 = x2 ® x1	–	+	–	–	–
f13 =`x1	–	–	+	–	+
f14 = x1 ® x2	–	+	–	–	–
f15 = x1 ½ x2	–	–	–	–	–
f16 = 1	–	+	+	+	+

В таблице 2.6 дается полезная информация о свойствах всех функций двух переменных. Пользуясь этой таблицей можно проверить полноту заданной системы функций, а также построить другие базисы.

Теорема о полноте даёт ответ на вопрос, из какой системы функций можно получить в виде суперпозиции любую функцию. Но в практических задачах нужна не столько возможность, сколько правила, пользуясь которыми можно получить представление, оп­тимальное в некотором смысле. Каждое представление функции в виде суперпозиции можно охарактеризовать некоторым числом, которое называется сложностью данного представления (напри­мер, число применений операции суперпозиции) и зависит от кон­кретной задачи. Тогда можно поставить задачу об отыскании пред­ставления логической функции наименьшей сложности. В принципе, такую задачу всегда можно решить последовательным перебором различных суперпозиций функций системы.

Рассмотрим теперь су­перпозиции над булевой системой функций, содержащей лишь конъюнкцию, дизъюнкцию и отрицание. Именно для этих суперпозиций методы минимизации разработаны достаточно хорошо. Чтобы дать точную формулировку задачи, приведем некоторые определения.

Минимальной ДНФ функции f(x₁,..., x_n) называется ДНФ N = U₁ Ú U₂ Ú... Ú U_k, представляющая функцию f(x₁,..., x_n) и содер­жащая наименьшее количество букв по сравнению с другими ДНФ, то есть число букв в N равно 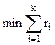, где r_i – ранг конъюнкции U_i, а минимизация проводится по всем ДНФ функции f(x₁,..., x_n).

Тогда задача об отыскании представления функции наименьшей сложности формулируется так: для всякой функции найти представление в виде минимальной ДНФ.

Прежде чем описать метод решения задачи дадим ещё несколь­ко определений.

Импликантом функции f(x₁,..., x_n) называется эле­мен­тарная конъюнкция 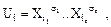если выполнено соотношение U_i ® f(x₁,..., x_n) º 1. Это означает, что если на некотором наборе импликант U_i обращается в единицу, то функция f(x₁,..., x_n) на этом наборе тоже обращается в единицу. Любая элементарная конъюнк­ция произвольной СДНФ является импликантом данной функции.

Простым импликантом функции f(x₁,..., x_n) называ­ется им­пликант функции f(x₁,..., x_n), если элементарная конъюнкция, полу­чающаяся из него удалением любой буквы, не является импликан­том функции.

Сокращенной ДНФ функции f(x₁,..., x_n) называется дизъюнк­ция всех простых импликантов функции f(x₁,..., x_n).

Теорема 5 (без доказательства). Сокращённая ДНФ представляет функцию f(x₁,..., x_n).

Теорема 6 (без доказательства). Минимальная ДНФ функции f(x₁,..., x_n) получается из ее сокращённой ДНФ удалением некото­рых элементарных конъюнкций.