| Процесс | Порядок захвата ресурсов | Порядок освобождения ресурсов |
| A | 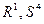
| S, R |
| B | 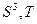
| T, S |
| C | 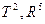
| T, R |
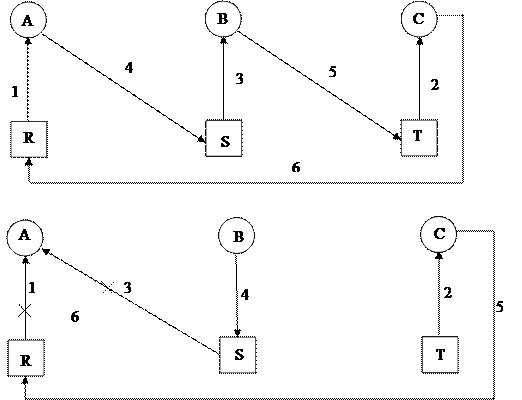 |
Последовательность: 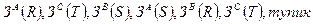
Последовательность: 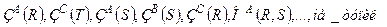
Здесь 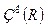 – захват потоком A ресурса R;
– захват потоком A ресурса R; 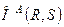 – освобождение потоком A ресурсов R и S.
– освобождение потоком A ресурсов R и S.
Вывод:
1) тупики возникают не при каждом исполнении;
2) аккуратным планированием можно избежать блокировок;
3) блокировки можно обнаружить;
Стратегии борьбы с блокировками
1. «Страусовый алгоритм»:
Допущение, что блокировки в системе можно игнорировать. Усилия, затраченные на преодоление блокировок, могут себя не оправдать.
2. Обнаружение и устранение:
Дать возможность произойти блокировке, обнаружить ее и предпринять действия для ее исправления.
Способы восстановления:
- принудительная выгрузка ресурса;
- восстановление через откат (прежде чем захватить ресурс, процесс сохраняет свое состояние (checkpoint, контрольная точка), в случае конфликта можно вернуться к сохраненному состоянию);
- выгрузить процесс целиком (если нет побочных эффектов (процесс не влияет на состояние системы)).
Обнаружение тупика в случае единственности ресурса каждого типа:
1) В текущем состоянии построить граф Холта;
2) Обнаружить на нем цикл по какому-либо алгоритму:
| Процесс | Захват ресурса | Ждет ресурс |
| A | R | S |
| B | - | T |
| C | - | S |
| D | V | S, T |
| E | T | V |
| F | W | S |
| G | V | U |
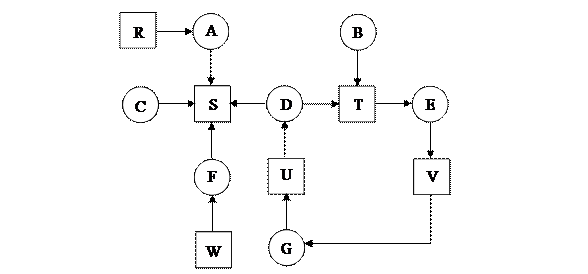
Алгоритм:
Выполняется для каждой вершины графа, в начале все ребра не маркированы.
1. Список посещенных вершин пустой, выбираем начальную вершину M.
2. M добавляем в список. Если M в списке есть, то обнаружен цикл.
3. Если у M имеется немаркированное исходящее ребро, то идем к шагу 4, иначе – к шагу 5.
4. Выбираем любое немаркированное ребро, маркируем его, переходим к новой вершине и объявляем её текущей; переходим к шагу 2.
5. Удаляем последнюю вершину из списка, выбираем ее текущей, переходим к шагу 3.
Обнаружение тупика, если имеется несколько ресурсов каждого типа:
(E 1, E 2, …, Em)= E – вектор ресурсов;
Ej - сколько ресурсов типа j (1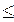 j
j 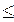 m)
m)
(A 1, A 2, …, Am)= A – вектор доступных ресурсов
Матрица текущего распределения ресурсов:
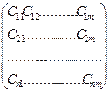 , где
, где 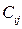 – сколько процесс i получил ресурсов типа j.
– сколько процесс i получил ресурсов типа j.
Матрица запросов ресурсов:
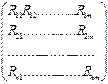
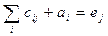
Алгоритм:
Все процессы не маркированы:
1) В матрице R ищем строку, соответствующую немаркированному процессу, которая меньше либо равна А, (ri 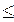 A).
A).
2) Если такая строка найдена, то маркируем процесс, прибавляем строку к вектору А, возвращаемся к шагу 1.
3) Если процессов нет, то конец.
Если находятся немаркированные процессы, то они в тупике.
Пример: Находится ли система в тупике?
E=(4, 2, 3, 1) A=(2, 1, 0, 0)
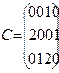
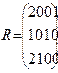
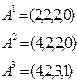
 2014-02-17
2014-02-17 716
716








