Лекции по гидравлике. border="0" />заменим эквивалентной величиной, где h -погружение точки М под уровень свободной поверхности жидкости (измеряется по вертикали)

border="0" />заменим эквивалентной величиной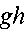, где h -погружение точки М под уровень свободной поверхности жидкости (измеряется по вертикали). Эти две величины

одинаковы, т.к. 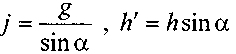. После этих преобразований уравнение равновесия

жидкости в цистерне примет привычный вид, соответствующий записи основного закона гидростатики:

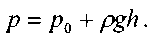
Таким образом, давление в любой точке жидкости будет зависеть только от положе­ния этой точки относительно уровня свободной поверхности жидкости. Поверхности рав­ного давления будут параллельны свободной поверхности жидкости, и иметь такой же ук­лон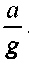

Равновесие жидкости в равномерно вращающемся сосуде. Свободная поверхность жидкости, залитой в цилиндрический сосуд и находящейся под действием сил тяжести примет форму горизонтальной плоскости на некотором уровне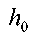относительно дна сосу­да. После того как мы приведём сосуд во вращение вокруг его вертикальной оси с некоторой постоянной угловой скоростью со = const, начальный уровень свободной по­верхности жидкости изменится: в центре сосуда он пони­зится, а по краям сосуда повысится. При этом форма сво­бодной поверхности примет явно вид криволинейной по­верхности вращения. Это явление объясняется тем, что 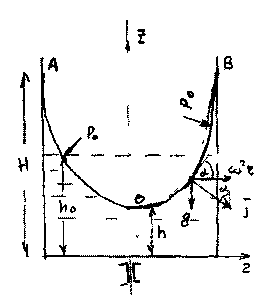при вращении сосуда вокруг своей оси жидкость в нём бу­дет испытывать ускорение переносного движения 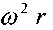направленное в сторону стенок сосуда. Поскольку равнодействующая двух сил: силы тя­жести и центробежной силы должна быть направлена по нормали к свободной поверхно­сти жидкости в каждой точке поверхности, то эта равнодействующая будет иметь, как быль сказано выше, две составляющие соответственно силу тяжести, направленную вер­тикально вниз и центробежную, направленную в горизонтальной плоскости.

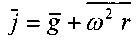
В каждой точке свободной поверхности жидкости АОВ вектор углового ускорения 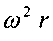будет направлен под некоторым углом а по отношению к касательной плоскости, проходящей через данную точку свободной поверхности.

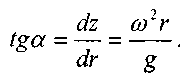
Отсюда:

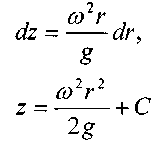
В центре на оси вращения, на расстоянии 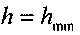от дна сосуда будет расположена

самая низкая точка свободной поверхности жидкости, т.е.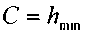

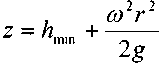
Отсюда: свободная поверхность жидкости находящейся в равномерно вращающемся вокруг его вертикальной оси сосуде будет иметь вид параболоида вращения (кривая АОВ- парабола).

Выберем любую точку жидкости на глубине под свободной поверхностью h (в част­ности точка находится на дне сосуда), тогда давление в ней будет равно:

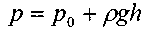
Этот вывод можно распространить и на более сложные случаи вращения сосуда, на­клоняя ось его вращения под углом к горизонту; результат получим тот же, что подтвер­ждает универсальность формулы основного урав­нения гидростатики.

2.4. Дифференциальное уравнение равнове­сия жидкости

После рассмотрения некоторых частных слу­чаев равновесия жидкости рассмотрим общее диф­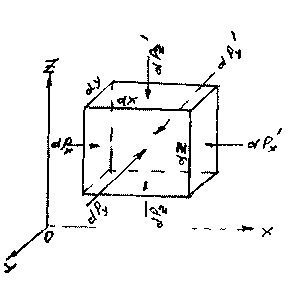 ференциальное равновесия в самом общем виде. Для этой цели выделим отсек жидкости малых раз­меров в виде параллелепипеда. Масса жидкости в выделенном объёме:

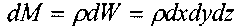
На боковые грани параллелепипеда действуют силы давления: (на левую и правую грани соответственно):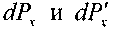. На переднюю и заднюю грани: 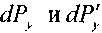, на нижнюю

и верхнюю грани: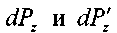

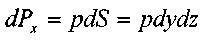
Поскольку давление на правую грань больше, то i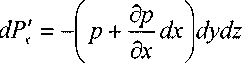

По аналогии можно записать силы давления на остальные пары граней.

на переднюю 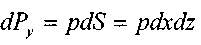, на заднюю 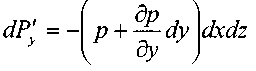, на нижнюю

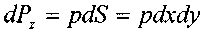, на верхнюю 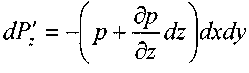Проекции массовых сил на координатные оси:

на ось ОХ будет на ось ОУ будет

на ось OZ будет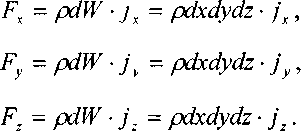 Тогда сумма сил действующих вдоль оси ОХ:

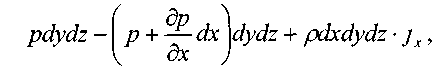
сумма сил действующих вдоль оси 07:

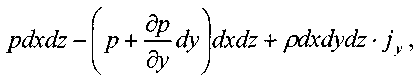
сумма сил действующих вдоль оси OZ:

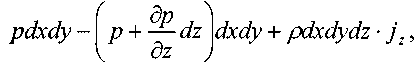
где: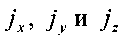, проекции ускорения массовых сил на координатные оси.

После преобразования получим систему дифференциальных уравнений равновесия жидкости:

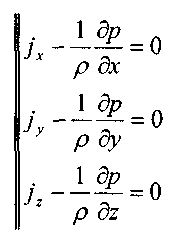i i >